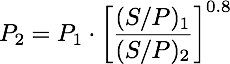The S/P ratio has been explained before on this website. Now two Technical Memorandums (TM 12-12 and TM 24-13) of the Illuminating Engineering Society of North America (IESNA) elaborate on how and how much advantage one can make on using light with a high S/P ratio.
The S/P ratio has been explained before on this website. Now two Technical Memorandums (TM 12-12 and TM 24-13) of the Illuminating Engineering Society of North America (IESNA) elaborate on how and how much advantage one can make on using light with a high S/P ratio.
In short it comes down to this: at low environmental light levels (such as in streets at night with street lights on) your eye works with night vision (you loose the colors in your view but still can see a lot of details and overview with only moon light and light from stars). Lamps with a specific light (a specific spectrum) suited for this night vision (meaning high S/P ratio) will lead to an increase of brightness perception. So we need less light for the same brightness impression.
A second effect is valid for light levels indoor (reading, work on computer, work on electronic and mechanic setups, repairing things etc). When you use light with a high blue content (cold white, meaning also high S/P ratio) then this results in a decrease of pupil size which results in a sharper view. Thanks to this the average light level can go down to still have the same view-efficiency.
Advantage with a higher S/P ratio, the TM 12-12
Light with a higher S/P ratio has an advantage in two ways, according to the mentioned TMs. The TM 12-12 now first. The name of this document is “Spectral Effect of Lighting on Visual Performance at Mesopic Lighting Levels”.
Mesopic light levels
The TM 12-12 talks about the higher sensitivity of rods at environments where a low lighting level is present. Such environments are called mesopic, where the average luminances over the full field of view is between 0.001 cd/mˆ2 until 5 cd/mˆ2. These are for instance outdoor areas on the public roads during the night, when using only streetlights (not city centers with a lot of building and advertisement/commercial lights).
Since rods are more sensitive as cones, when we are in an area with mesopic light levels where also rods play a role in the brightness impression we have, we could get a higher brightness impression than with cones alone (which is the standard measurement convention, to only use the cones response).
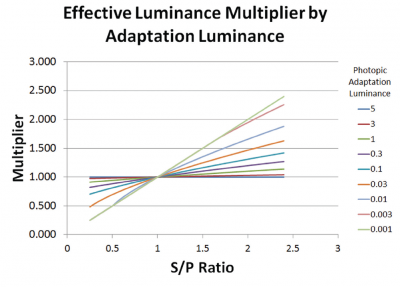
The TM introduces a multiplication factor (the Effective Luminance Factor or in short ELF) that indicates that the benefit is bigger at lower background luminances at that this approaches the value S/P ratio when mesopic goes into scotopic (less than 0.001 cd/mˆ2). And that this ELF value goes towards 1 when the background illuminance reaches the photopic illuminances, from 5 cd/mˆ2.
Note I: the TM recognizes that the rods are (almost) not present in the fovea, there where we focus and see colors (the area of the cones). Still the TM takes the possible positive effect of a high(er) S/P ratio as valid for the whole view area, including the small area of 2 degrees called the fovea. When considering the tasks concerned (driving or walking at night) it is the complete view that counts where the periphery is very important as well. Therefore the improvement in brightness impression brought by the rods counts as a general improvement for the whole view.
Note II: The TM gives a calculation method that computes the effective luminance for (relevant) parts of the field of view. This is what is they call a point-to-point calculation; parts with a different light intensity than other areas are then well taken into account.
Calculation method
The TM defines a set of steps to determine the effective luminance (L_effective, which can be calculated into an effective illuminance E_effective). Take note that this is a point-to-point calculation where the field of view is divided into smaller parts with each a distinct average illuminance value.
Step 1: determine the desired illuminance value (from desin), the E_design (lux).
Step 2: determine for a surface in the field of view the reflection factor rho.
Step 3: calculate the resulting luminance:
Step 4: calculate the conventional (based on photopic quantities) illuminance E_photopic. One can use for this the normatives or guidelines that exist (for outdoor).
Step 5: compute L_photopic:
Step 6: use the Effective Luminance Factor (ELF) to compute the L_effective from the L_photopic):
Step 7: adapt the design such that L_effective = L_design.
Step 8: If an illuminance value is needed it can be computed:
The Effective Luminance Factor (ELF)
This factor is used to determine the effective luminance (cd/mˆ2) or the effective illuminance value (lux). This factor is depending on the S/P ratio of the light source and of the photopic adaption luminance (that area where the eye is adapted to, which can be differently for local areas with different local luminance).
Table with multiplier (ELF) as a funciton of S/P ratio and local photopic adaptation luminance.
The ELF is about 1 for higher photopic adapted luminances (5 cd/mˆ2 or more) and approaches the S/P ratio for very low local photopic adapted luminances (0.001 Cd/mˆ2 or less).
Local and global
The computation of the ELF value needs to be done for local areas. Since the eye can have different adaptation states for different areas in one complete field of view. A global average effective luminance (if needed) can be computed by taking the average of all the local effective luminances.
The point-to-point computation of an ELF value results in a more homogeneous result for L_effective than L_photopic; the ELF value is higher for low L_photopic (when considering high S/P ratios) so differences between high and low L_photopic get attenuated a bit via ELF values when computing the L_effective.
A number of issues that need some more research
A few of these taken from the TM:
Glare – at low adaptation luminances glare is more intrusive than at high adapation luminances.
Chromatic effects – color can lead to additional performance of the scene looked at has low contrasts.
Age of observer – it appears that the yellowing of the lens with age does not have a significant effect on the difference in brightness perceived by the S/P ratio in mesopic circumstances.
Head lights effects – high intensity discharge (HID) head lamps that are more and more used in cars, lead to a lot of complaints about glare from oncoming vehicles. Little is known about the adaptation state of a visual system during the driving task so not much can be said about the effect of head lights.
Advantage with a higher S/P ratio, the TM 24-13
Light with a higher S/P ratio has an advantage in two ways, according to the mentioned TMs. The TM 24-13 as second. The name of this document is “(an optional method for) Adjusting the Recommended Illuminance for Visually Demanding Tasks Within IES Illuminance Categories P through Y Based on Light Source Spectum”.
Light levels indoor and pupil size
This TM is about more effective visual efficiency when light with high S/P ratio is used. It states that, by using light with high S/P ratio, the (big) blue part of the light leads to a smaller pupil size. This smaller pupil size leads to a bigger focus depth. This has a positive effect on tasks that require a lot of the visual system, for instance reading, repairing goods, analyzing goods etc (seeing and recognizing details).
We need sufficiently high light levels to use this effect, which means a background illuminance of minimally 50 cd/mˆ2.
The statement is that, when using light with high S/P ratio, we can do with less light (with lower S/P ratio), when we consider the following:
– tasks that are demanding visual tasks
– tasks the use a full field of view (including the rods)
– where an amount of light is used that is enough to see the details needed, but not too much that we are in a so called comfort zone (visual efficiency) where a small decrease in light does not impact the performance.
Calculation of Equivalent Visual Efficiency (EVE) factor
Given a photopic light level ‘A’ under an illuminant ‘x’ of a known S/P value (A(x)), there may be an alternative illuminant ‘y’ with a different S/P value that can provide the same level of visual acuity but with a different photopic light level ‘B’ (B(y)). The two different photopic light levels (A(x)) and (B(y)) are then providing equivalent visual efficiency.
Quantified:
P_1 is the photopic light level of a light source that is normally used in the considered application and P_2 is the level needed in the same application, where we have the same visual acuity and where we use a light source with different S/P ratio. So we calculate a new photopic light level using as a basis the standard light source and a comparison of the standard S/P ratio and the S/P ratio of the new light source.
P can represent different physical quantities and is based on the V(lambda) curve: lumen, lux, cd/mˆ2.
example calculation:
A comparison between a 3500 K fluorescent Tube Light (S/P here taken as 1.4) and a led tube light of 5000 K (S/P here taken as 2.0) as the replacer. The application is indoor work in an industrial environment where the tasks are visually demanding.
The needed illuminance when using led tubes in this application is then: 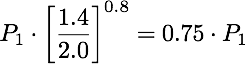 which means 75 % of the original illuminance value.
which means 75 % of the original illuminance value.
Since visual efficiency is kept constant, also the original task performance is.
Table with EVE multiplication factors:
In the TM there is a table which takes as base a default light source with S/P ratio of 1.4 (representing a typical halogen or fluorescent tube light of 3500 K CCT). This is representative for many indoor illumination schemes where visually demanding tasks are being done as normal work (including full field of view and background illuminance is minimally 50 cd/mˆ2). The table then shows the EVE values with this S/P = 1.4 as a basis. The relative multiplication factors for light sources with an S/P ratio different than S/P = 1.4 are calculated and these factors can be used to calculate the corresponding light level for the source of different S/P ratio.
Note: if in a certain situation the reference lamp that needs to be replaces, has a different S/P ratio, then a new EVE value can be computed using equation (V) using the current lamp’s S/P ratio and the S/P ratio of the lamp that will replace it.
The multiplication factor in the table can be used to compute either equivalent luminance, luminous flux or illuminance (respectively in cd/mˆ2, lumen, lux).
| S/P ratio | EVE factor | . | S/P ratio | EVE factor |
|---|---|---|---|---|
| 0.6 | 1.97 | . | 1.5 | 0.95 |
| 0.7 | 1.74 | . | 1.6 | 0.90 |
| 0.8 | 1.56 | . | 1.7 | 0.86 |
| 0.9 | 1.42 | . | 1.8 | 0.82 |
| 1.0 | 1.31 | . | 1.9 | 0.78 |
| 1.1 | 1.21 | . | 2.0 | 0.75 |
| 1.2 | 1.13 | . | 2.1 | 0.72 |
| 1.3 | 1.06 | . | 2.2 | 0.70 |
| 1.4 | 1.0 | . | 2.3 | 0.67 |
Note: the possible gain in decreasing the illuminance (or luminance or lumen) without impact on the visual efficiency is because of the decrease of the pupil size. It appears the S/P ratio to the power of 0.8 is a good approximation of this effect. It can be that in future a more precise determination is found for this gain (different equation) such that the equation (V) will be adapted.
Analysis of research done in this field
The TM has analyzed a number of researches done in this field which show that this relation between pupil size and S/P ratio and gain or loss in visual efficiency is applicable. They have seen that in working areas where light sources of 3000 K were used and were replaced by 5000 K, that the amount of light could be reduced to the S/P^0.8 factor without impact on error rates in the work done or on work speed. People also accepted the light of 5000 K (up to 6500 K was reported to be accepted).
A number of researches did not find or enforce that the above determined relation of S/P ratio and gain in light quantity is valid, but analysis showed that these researches did not take into account the following necessary conditions:
– it concerns a task where the full view is used for. So not only the receptors in the foveal area.
– it concerns a task where the eye is fully adapted to, such that the pupil size has been adapted to it. Indoor lighting and its work tasks do normally have a constant background luminance and task lighting so that fulfills this requirement.
– a correct comparison between light spectrum and light level. When a comparison is to be done then the variation in light level and S/P ratio needs to be in the order of the applied equation 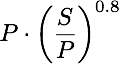 . So not researches that used much bigger variations, since in that case the pupil size can not follow such variations any more and hence cannot compensate for it. Besides this, the variation must be enough to result in a significant effect on performance; so we not need to be in an environment with such a lot of light that a light reduction does not lead to loss of performance.
. So not researches that used much bigger variations, since in that case the pupil size can not follow such variations any more and hence cannot compensate for it. Besides this, the variation must be enough to result in a significant effect on performance; so we not need to be in an environment with such a lot of light that a light reduction does not lead to loss of performance.
– it concerns a task that is visually demanding, so requiring high visual acuity. When this is the case, the variation of the light quantity as well as its spectral composition does have a (measurable) effect on the visual performance.
– the distance to the task remains constant. With this is assured that the field of view is not impacted and remains a full field of view.
Conclusions
The two mentioned Technical Memorandums (TMs) show that a gain is obtained when applying light with high S/P ratio; one can decrease the illuminance, luminance of lumen total and get the same light impression or visual efficiency when applying light sources with higher S/P ratio that the ones used before.
Both TMs come with a calculation model that show in what way it can be used quantitatively.
The TMs have both its own application area and light levels; one for mesopic light levels (mostly outside but can be also inside in parking lots) and the other for illumination applications indoor.
The background of both TMs also differs: one explains that the rods contribute to the improvement of the brightness perception and the other explains that a reduction of pupil size leads to a gain in visual efficiency. The result is that in both cases the illuminance, luminance or lumen total can be reduced in order to keep the perception or visual efficiency the same.