In voorgaande artikels (metingen aan ledlampen II en metingen verbruik nieuwe server) heb ik gesproken over de powerfactor. Ik kreeg de vraag om dit eens uit te leggen, vandaar dit artikel.

Definitie powerfactor
De powerfactor PF zegt iets over de relatie tussen het netto vermogen P en het schijnbaar vermogen S. Het is namelijk de deling van het vermogen door het schijnbaar vermogen.
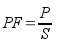
De PF is een meetlat die aangeeft hoe efficiënt elektrisch vermogen wordt afgegeven aan de verbruiker (bijvoorbeeld een computer, of een oven of een tv of iets dergelijks). Idealiter is de PF gelijk aan 1. En alles lager dan 1 betekent dat er extra vermogen nodig is om het gewenste vermogen aan de verbruiker af te geven.
vermogen P [W] Het netto vermogen P is dat vermogen waarvoor we moeten betalen aan het energiebedrijf. Een voorbeeld: wanneer je een 100 W lamp hebt en je zet deze aan, dan is het zo dat je een vermogen trekt van P = 100 Watt. Laat je deze lamp 10 uur aan, dan heb je een hoeveelheid energie van 10 uur x 100 W = 1 kWh afgenomen, en daarvoor betaal je nu zo’n 20 cent (energie is dus vermogen maal de tijdsduur).
schijnbaar vermogen S [VA] Het schijnbaar vermogen S is vermogen dat nodig is om P af te geven. Nu wordt het wat technisch, maar wanneer je een gewone gloeilamp hebt (eigenlijk een gewone weerstand), dan is S gelijk aan P. Echter, wanneer je wat meer ingewikkelde elektronica hebt zoals een geschakelde computervoeding, dan zal S groter zijn dan P. Alles wat S groter is dan P is niet netto vermogen, maar is energie die heen en weer gaat tussen het net en de verbruiker (bijvoorbeeld de computervoeding) en die nodig is om de computervoeding goed te laten werken.
Het is dus stroom die heen door de draden stroomt en weer terug. Omdat de stroom ook weer terugstroomt, is er netto geen energie afgenomen en is dus geen netto afgegeven energie (P is dan nul).
Een voorbeeld: je hebt een computervoeding die een computer voedt en deze computer vraagt 100 W. Nu moet dus minimaal deze 100 W door de computervoeding heengaan. Maar omdat de computervoeding zelf ook wat energie nodig heeft om goed te werken, gaat er iets meer aan vermogen in, stel bijvoorbeeld 10 W extra. Nu is er echter nog iets aan de hand, want de computervoeding heeft ook nog eens wat energieuitwisseling met het net, om intern goed te werken (bijvoorbeeld het magnetiseren en demagnetiseren van spoelen, het laden en ontladen van condensatoren etc). De stroom die hiervoor gebruikt wordt, wordt ook weer teruggegeven aan het net. Daardoor is het netto vermogen nul van dit gedeelte.
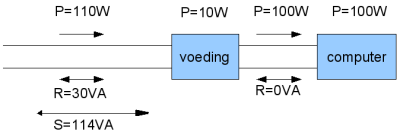
Je ziet vanuit het net gezien, een vraag van P=110W en een vraag van R (reactief vermogen)=30VA. Reactief vermogen is precies dat vermogen dat nodig is voor de op- en afbouw van magnetische velden en ladingen in de voeding. Dit reactieve vermogen wordt heen en weer gestuurd van en naar het net en per saldo is het geen netto vermogen. Dus als prive verbuiker betaal je er ook niet voor. Schijnbaar vermogen S is dan de optelling van deze twee, maar dan wel vectorieel.
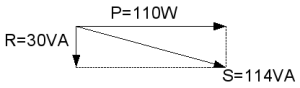
Vectoriële optelling is dan de wortel uit de som van het kwadraat van P en R, en levert bij waardes 110 en 30 dan het resultaat van 114 VA op. Het is nu ook duidelijk dat, wanneer R = 0, dat dan geldt S = P. Wanneer R > 0, dan geldt S > P. Omdat PF de deling van P door S is, geldt dus voor de PF ≤ 1.
Update 11 mei 2016: let op, dit hiervoorgenoemde blindvermogen is het vermogen van de grondharmonische voor zover deze uit fase is met de spanning, maar ook het vermogen van alle hogere harmonischen van de stroom.
Powerfactor als totaal van faseverschuiving en ongelijkvormigheid
Je kunt de powerfactor ook zien als het totaal van niet optimale overeenstemming tussen spanning en de stroom die resulteert wanneer de verbruiker aan de spanning wordt gesloten.
Stel we hebben een mooie sinusvormige netspanning. Deze is normaliter 230V AC met 50 Hz en sinusvormig. Wanneer we de verbruiker aansluiten dan volgt een bepaalde stroom. Als deze stroom mooi sinusvormig is maar niet in fase met de spanning, dan is de powerfactor dus lager dan 1.
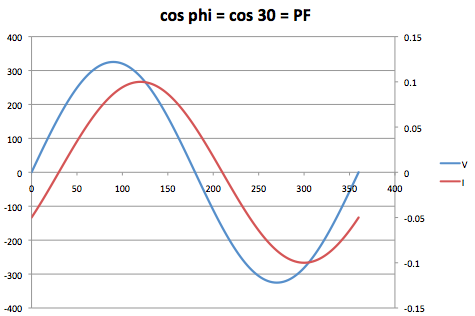
De powerfactor is nu gelijk aan de cosinus phi, waarbij de phi het faseverschil is.
Echter er kan ook sprake zijn van een ongelijkvormigheid.

In het bovenstaande plaatje zie je de stroom als piek, en niet sinusvormig als de spanning. De piek van de stroom komt overeen met de piek van de spanning, dus de fase hierbij is wel gelijk. Maar door de ongelijkvormigheid is de powerfactor toch kleiner dan 1. Men zou het zo kunnen zien: de stroomvorm is op te bouwen uit een aantal sinus-componenten: 1 comonent met de gelijke frequentie als de spanning en dan een hele reeks componenten met een hogere frequentie, de zogenaamde harmonischen. Deze harmonischen zorgen ervoor dat er vermogen heen en weer gaat zonder verbruik, dus een lagere powerfactor.
Er is ook een gecombineerd effect mogelijk:

In dit geval is stroom niet gelijkvormig, noch dat ze in fase zijn. De powerfactor verdisconteert beide effecten en 1 waarde, in dit geval weer kleiner dan 1.
Impact van de PF
Nu weten we dat de PF maximaal 1 kan zijn, en dat in het geval dat reactieve vermogen R = 0. We weten ook dat we als prive gebruiker alleen voor P betalen, omdat dat vermogen is wat we opsouperen. Voor R betalen we niet, want dat is vermogen dat heen en weer fietst tussen het net en de verbruiker. Grootvebruikers als grote bedrijven met hoge vermogensaansluitingen betalen echter wèl wanneer R te groot wordt. De impact is namelijk dat er voor die vermogensuitwisseling als gevolg van R wèl stromen lopen, en die stromen lopen weer door kabels. De extra stromen als gevolg van R die dus door de kabels lopen, vereisen dat de kabels dikker gemaakt worden dan strikt noodzakelijk was voor de levering van het netto vermogen P. Verder is het zo dat iedere stroom door een kabel, ook een verlies oplevert (Ohmse weerstand door de kabel). Voor zover deze Ohmse verliezen in ons huis optreden, betalen we ervoor omdat dit weer netto afgeleverd vermogen P is. Maar de stromen lopen ook door het net (vòòr onze meter) en dan is het het verlies van de elektriciteitsleverancier.
Een klein rekenvoorbeeld van deze verliezen. Stel we hebben de situatie dat ik een mooie Ohmse belasting heb en die trekt een vermogen P. Nu geldt dus S = P (R = 0) en de stroom die loopt is precies de stroom nodig voor het leveren van P, noem deze stroom eens Ip (=Is). Het Ohmse verlies agv de stroom Ip in het net is dan Rnet*(Ip)2, en Rnet is de weerstand van het net. Dit verlies is echt vermogensverlies en is ten koste van de vermogensleverancier.
E.e.a. in een tabelvorm:
| PF | Is/Ip | Pverlies_s/Pverlies_p |
|---|---|---|
| 1 | 1 | 1 |
| 0,9 | 1,11 | 1,11 |
| 0,8 | 1,25 | 1,25 |
| 0,7 | 1,43 | 1,43 |
| 0,6 | 1,67 | 1,67 |
| 0,5 | 2 | 2 |
| 0,4 | 2,5 | 2,5 |
| 0,3 | 3,33 | 3,33 |
Aldus een niet gunstige powerfactor, die veel kleiner is dan 1, zorgt ervoor dat er grotere stromen lopen dan dat het strikt noodzakelijk was voor het afgeleverde netto vermogen, en deze grotere stromen zorgen nu voor meer verlies in de leidingen van het aanvoernet.
Lage PF betekent hogere verliezen in het aanvoernet
Hogere stromen zorgen ook voor grotere spanningsval in het aanvoernet, wat betekent dat de spanning zoals die binnenkomt bij de eindverbruiker lager is. Dit is ongunstig voor bijvoorbeeld lampen, die minder sterk branden.
Lage PF betekent een hogere spanningsval in het aanvoernet
Deze hogere stromen moeten echter wel geleverd worden, en daarvoor zijn wel grotere generatoren nodig (aan de generatiekant van het net) dan wanneer ik geen R-stromen had gehad.
Lage PF betekent ook grotere generatoren voor het genereren van de hogere stroom
Wanneer je als gebruiker een aftap hebt van 1 x 35 A, maar je PF is maar 0,5, dan haal je maar de helft aan het netto vermogen uit je aftap. Want 1 x 35 A bij 230 V zou maximaal een vermogen van 230 V * 35 A = 8050 W zijn. Maar wanneer je PF 0,5 is, dan geldt dat Is = 35 A en Ip = 17,5 A, dus je haalt maar 4025 W uit je aftap. Wil je meer, dan moet je of je PF corrigeren of een grotere aftap huren en dus meer betalen.
Lage PF betekent dat je minder netto vermogen uit je aftap kunt halen
De verliezen agv hogere stromen binnenshuis van een eindverbruiker zijn niet zo groot, omdat de lengte van de leidingen niet zo lang zijn. Maar het feit dat er hogere stromen lopen, betekent ook dat de verbruikers zelf, en de componenten die met deze hogere stromen te maken krijgen, wat de levensduur van deze componenten verkort.
Lage PF betekent hogere stromen en meer belasting voor de componenten, dus een kortere levensduur




62 reacties op “De powerfactor uitgelegd”
Laatst was ik in een grote fabriek waar ze reserve transformatoren hebben, met condensatorcompensatie. De reserve transformatoren staan aan en de condensatoren ingeschakeld. Gaat hun dit geld kosten (warmteverliezen) of compenseert het de arbeidsfactor van de gebruikte installatie.
Alvast bedankt voor de reactie.
Groeten, Jelle
Jelle. Blindstroom an sich zijn die stromen die het blindvermogen heen en weer transporteren. Omdat er geen netto vermogen is, wordt er dus voor vermogensafname niet betaald.
ECHTER: als er een stroom loopt, ook al is het een blindstroom, dan ontstaat er toch wat warmte als gevolg van de weerstand van de kabels. Die warmte is wel degelijk vermogen (we noemen het hier verlies) en daarvoor moet worden betaald (tenminste, als die warmte achter je eigen meter gebeurt. Alle warmte vóór je meter wordt natuurlijk niet meegemeten en betaal je dan niet voor).
DUS: je begint te denken aan een pure blindstroom, dat wil zeggen een stroom die 90 graden uit fase is met de spanning. Dan zal er als gevolg van die blindstroom toch wat verlies in de kabels optreden en daardoor is de blindstroom geen pure blindstroom meer maar bevat een klein beetje actieve stroom. Dus het faseverschil is niet precies 90 graden maar iets kleiner.
Als je een groot bedrijf bent en een grote elektriciteitsaansluiting hebt (ik ga even uit van 3×90 A en hoger), dan zul je moeten voldoen aan een door de netbeheerder gestelde eis van een minimale powerfactor van ik geloof 0.85. Lig je daaronder dan betaal je boete, of mogelijk dat ze je direct laten betalen voor blindvermogen.
Installeer je nu condensatorbanken om de blindstromen die komen van grotere motoren, te compenseren, dan beperk je de blinstromen tot tussen de motoren en je eigen transformatoren. Daarom bestaat er dus ook alleen maar wat warmte in de leidingen tussen motoren en transformatoren/condensatorpakket. En het is die warmte (klein) waarvoor je betaalt.
Zou je geen condensatoren hebben, dan zou de blindstroom ook nog lopen tot voorbij je transformatoren en dan geldt een klein verlies ook voorbij de transformatoren. Echter misschien voldoe je dan niet meer aan de eis van de netbeheerder van een minimale powerfactor, of je betaalt voor meer blindstroom.
Hallo Marcel,
Bedankt voor je antwoord, maar wat ik nog niet weet of het helpt om een transformator, die verder niet gebruikt wordt, om daar een condensatorcompensatie op aan te sluiten. Wat mij opviel is dat die condensatorkast erg warm werd. Volgens mij kun je beter compenseren bij de transformatoren die wel gebruikt worden, of nog beter bij de veroorzaker.
Je kunt dan de trafo ook zien als een inductieve belasting en die compenseren dmv een condensator aan zijn ingang
Daarmee compenseer je het beetje inductiviteit die de trafo heeft en de blindstromen blijven dan beperkt in het gebied tussen condensator en ingang vd nietsdoende trafo.
Verder is het waar om de blindstromen te voorkomen en bij de verbruiker zelf de compensatie aan te brengen. Dat gaat nig bij hoofdzakelijk nductieve belastingen zoals bijvoorbeeld mijn eigen warmtepomp (vanwege de 2.6kW compressormotor).
Boven artikel 15 zie ik enkele slimmeriken die met gebruik van de PF gratis warmte willen onttrekken aan het net, dat zal nog niet mee vallen.
Wat misschien nog wel een mogelijkheid is met hulp van de buurvrouw de nul achter de meter ruilen met de buren, dan is de stroom gegarandeerd uit fase met de spanning, mits de buurvrouw op een andere fase zit dan jezelf.
Met een verschil van 120 graden zal het nooit 0 worden maar achteruit lopen is een mogelijkheid.
Je hebt het niet van mij he?
Reactie op “22”
Wat ik niet begrijp: als je van 100 Watt met PF 0.80 gaat naar een vermogen van 90 Watt (10% reductie), dat de PF dan mee verandert…
Bijvoorbeeld: van 20 LEDs met vermogen van 5 Watt er 2 uitschakelen.
Dank je Dirk
Hoi Dirk, je geeft niet aan welke PF er dan geldt bij je 90 Watt situatie.
Het feit dat het opgenomen vermogen omlaag gaat is te begrijipen. Als het allemaal leds met ieder een eigen voeding zijn, dan betekent afschakelen ook vermogensvermindering. Schakel ik 10 % af, dan ook 10 % vermogensvermindering. Echter de powerfactor behoort bij het gedrag van 1 voeding. Heb ik er 10 dan blijft het gedrag van het totaal hetzelfde. Dus ik zou verwachten dat de powerfactor niet noemenswaard verandert.
Dat zou anders kunnen zijn wanneer jij 10 ledlampjes achter 1 voeding hebt. Dan geldt voor het geheel een powerfactor. Echter bij het afschakelen van twee leds dan wordt de voeding zelf minder belast en gaat ook anders werken. In dat geval kan ook de powerfactor veranderen.
leid aan spanningsverlies en de stroom neem toe.
te veel onnodige energieverbruik,wanneer je PF kleiner wordt.
Behalve wanneer er ledlampen als belasting hebt. Betekent minder belasting of minder energie verbruik
Bij een inverter voor zonneenergie van AC naar DC staat ingang 6750 W en nominal 5000VA. Er is geen power factorgegeven in de specificatie.
Als de PF 1 is betekent dit dan van de 6750 W maar 5000 W omgezet wordt.
@A van Dongen. PF is 1 bij DC vermogens, en kan een waarde zijn van 0 tot 1 bij AC vermogens. Aan de DC kant hoeven we niet over PF te spreken. Die is toch 1. Wat ik bij mijn voedingen zie gespecificeerd, is wanneer ik een AC voltage genereer, dat ik dan een maximale 1750VA kan uitsturen. Dat betekent bi een PF=1 dat ik dan 1750 W uitvoer. Heb ik een PF van 0.9 dan voer ik maximaal 1750VA (= S) en bij een PF=1 is dat gelijk aan vermogen P = PF x S = 1575 W. Dus, bij een PF < 1 is het uitgevoerde vermogen P altijd kleiner dan S.
Bij jou staat 6750W en nominaal 5000VA, waarbij VA dus kleiner is dan 6750W. Ik kan dat niet verklaren.
Beste, is het mogelijk dat de PF groter dan 1 kan worden? want in de theorie is er aangegeven dat de max. waarde 1 is welke bereikt kan worden.
@mataw. De powerfactor is gelijk aan de verhouding netto vermogen gedeeld door schijnbaar vermogen. Dus PF = P / S.
Schijnbaar vermogen S het totaal aan vermogen, zowel netto als blindvermogen (wat vaak met Q aangegeven). Dit gaat dan als volgt: S^2 = P^2 + Q^2. De minimale waarde voor Q = 0 (er kan dus nul blindvermogen zijn, maar er kan geen negatieve blindvermogen zijn), dan geldt dat S^2 = P^2 en dus S = P, en dan volgt voor de PF = S/S = 1. Dit is dan meteen de maximale waarde.