In voorgaande artikels (metingen aan ledlampen II en metingen verbruik nieuwe server) heb ik gesproken over de powerfactor. Ik kreeg de vraag om dit eens uit te leggen, vandaar dit artikel.

Definitie powerfactor
De powerfactor PF zegt iets over de relatie tussen het netto vermogen P en het schijnbaar vermogen S. Het is namelijk de deling van het vermogen door het schijnbaar vermogen.
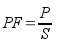
De PF is een meetlat die aangeeft hoe efficiënt elektrisch vermogen wordt afgegeven aan de verbruiker (bijvoorbeeld een computer, of een oven of een tv of iets dergelijks). Idealiter is de PF gelijk aan 1. En alles lager dan 1 betekent dat er extra vermogen nodig is om het gewenste vermogen aan de verbruiker af te geven.
vermogen P [W] Het netto vermogen P is dat vermogen waarvoor we moeten betalen aan het energiebedrijf. Een voorbeeld: wanneer je een 100 W lamp hebt en je zet deze aan, dan is het zo dat je een vermogen trekt van P = 100 Watt. Laat je deze lamp 10 uur aan, dan heb je een hoeveelheid energie van 10 uur x 100 W = 1 kWh afgenomen, en daarvoor betaal je nu zo’n 20 cent (energie is dus vermogen maal de tijdsduur).
schijnbaar vermogen S [VA] Het schijnbaar vermogen S is vermogen dat nodig is om P af te geven. Nu wordt het wat technisch, maar wanneer je een gewone gloeilamp hebt (eigenlijk een gewone weerstand), dan is S gelijk aan P. Echter, wanneer je wat meer ingewikkelde elektronica hebt zoals een geschakelde computervoeding, dan zal S groter zijn dan P. Alles wat S groter is dan P is niet netto vermogen, maar is energie die heen en weer gaat tussen het net en de verbruiker (bijvoorbeeld de computervoeding) en die nodig is om de computervoeding goed te laten werken.
Het is dus stroom die heen door de draden stroomt en weer terug. Omdat de stroom ook weer terugstroomt, is er netto geen energie afgenomen en is dus geen netto afgegeven energie (P is dan nul).
Een voorbeeld: je hebt een computervoeding die een computer voedt en deze computer vraagt 100 W. Nu moet dus minimaal deze 100 W door de computervoeding heengaan. Maar omdat de computervoeding zelf ook wat energie nodig heeft om goed te werken, gaat er iets meer aan vermogen in, stel bijvoorbeeld 10 W extra. Nu is er echter nog iets aan de hand, want de computervoeding heeft ook nog eens wat energieuitwisseling met het net, om intern goed te werken (bijvoorbeeld het magnetiseren en demagnetiseren van spoelen, het laden en ontladen van condensatoren etc). De stroom die hiervoor gebruikt wordt, wordt ook weer teruggegeven aan het net. Daardoor is het netto vermogen nul van dit gedeelte.
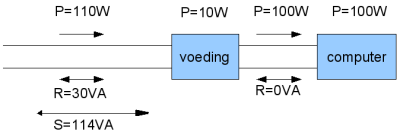
Je ziet vanuit het net gezien, een vraag van P=110W en een vraag van R (reactief vermogen)=30VA. Reactief vermogen is precies dat vermogen dat nodig is voor de op- en afbouw van magnetische velden en ladingen in de voeding. Dit reactieve vermogen wordt heen en weer gestuurd van en naar het net en per saldo is het geen netto vermogen. Dus als prive verbuiker betaal je er ook niet voor. Schijnbaar vermogen S is dan de optelling van deze twee, maar dan wel vectorieel.
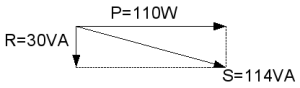
Vectoriële optelling is dan de wortel uit de som van het kwadraat van P en R, en levert bij waardes 110 en 30 dan het resultaat van 114 VA op. Het is nu ook duidelijk dat, wanneer R = 0, dat dan geldt S = P. Wanneer R > 0, dan geldt S > P. Omdat PF de deling van P door S is, geldt dus voor de PF ≤ 1.
Update 11 mei 2016: let op, dit hiervoorgenoemde blindvermogen is het vermogen van de grondharmonische voor zover deze uit fase is met de spanning, maar ook het vermogen van alle hogere harmonischen van de stroom.
Powerfactor als totaal van faseverschuiving en ongelijkvormigheid
Je kunt de powerfactor ook zien als het totaal van niet optimale overeenstemming tussen spanning en de stroom die resulteert wanneer de verbruiker aan de spanning wordt gesloten.
Stel we hebben een mooie sinusvormige netspanning. Deze is normaliter 230V AC met 50 Hz en sinusvormig. Wanneer we de verbruiker aansluiten dan volgt een bepaalde stroom. Als deze stroom mooi sinusvormig is maar niet in fase met de spanning, dan is de powerfactor dus lager dan 1.
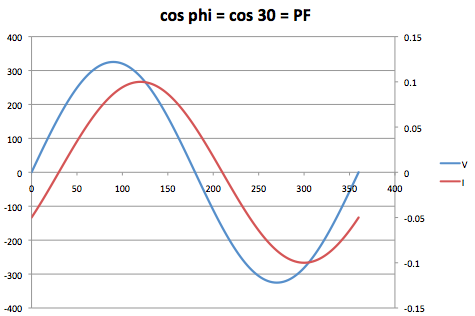
De powerfactor is nu gelijk aan de cosinus phi, waarbij de phi het faseverschil is.
Echter er kan ook sprake zijn van een ongelijkvormigheid.

In het bovenstaande plaatje zie je de stroom als piek, en niet sinusvormig als de spanning. De piek van de stroom komt overeen met de piek van de spanning, dus de fase hierbij is wel gelijk. Maar door de ongelijkvormigheid is de powerfactor toch kleiner dan 1. Men zou het zo kunnen zien: de stroomvorm is op te bouwen uit een aantal sinus-componenten: 1 comonent met de gelijke frequentie als de spanning en dan een hele reeks componenten met een hogere frequentie, de zogenaamde harmonischen. Deze harmonischen zorgen ervoor dat er vermogen heen en weer gaat zonder verbruik, dus een lagere powerfactor.
Er is ook een gecombineerd effect mogelijk:

In dit geval is stroom niet gelijkvormig, noch dat ze in fase zijn. De powerfactor verdisconteert beide effecten en 1 waarde, in dit geval weer kleiner dan 1.
Impact van de PF
Nu weten we dat de PF maximaal 1 kan zijn, en dat in het geval dat reactieve vermogen R = 0. We weten ook dat we als prive gebruiker alleen voor P betalen, omdat dat vermogen is wat we opsouperen. Voor R betalen we niet, want dat is vermogen dat heen en weer fietst tussen het net en de verbruiker. Grootvebruikers als grote bedrijven met hoge vermogensaansluitingen betalen echter wèl wanneer R te groot wordt. De impact is namelijk dat er voor die vermogensuitwisseling als gevolg van R wèl stromen lopen, en die stromen lopen weer door kabels. De extra stromen als gevolg van R die dus door de kabels lopen, vereisen dat de kabels dikker gemaakt worden dan strikt noodzakelijk was voor de levering van het netto vermogen P. Verder is het zo dat iedere stroom door een kabel, ook een verlies oplevert (Ohmse weerstand door de kabel). Voor zover deze Ohmse verliezen in ons huis optreden, betalen we ervoor omdat dit weer netto afgeleverd vermogen P is. Maar de stromen lopen ook door het net (vòòr onze meter) en dan is het het verlies van de elektriciteitsleverancier.
Een klein rekenvoorbeeld van deze verliezen. Stel we hebben de situatie dat ik een mooie Ohmse belasting heb en die trekt een vermogen P. Nu geldt dus S = P (R = 0) en de stroom die loopt is precies de stroom nodig voor het leveren van P, noem deze stroom eens Ip (=Is). Het Ohmse verlies agv de stroom Ip in het net is dan Rnet*(Ip)2, en Rnet is de weerstand van het net. Dit verlies is echt vermogensverlies en is ten koste van de vermogensleverancier.
E.e.a. in een tabelvorm:
| PF | Is/Ip | Pverlies_s/Pverlies_p |
|---|---|---|
| 1 | 1 | 1 |
| 0,9 | 1,11 | 1,11 |
| 0,8 | 1,25 | 1,25 |
| 0,7 | 1,43 | 1,43 |
| 0,6 | 1,67 | 1,67 |
| 0,5 | 2 | 2 |
| 0,4 | 2,5 | 2,5 |
| 0,3 | 3,33 | 3,33 |
Aldus een niet gunstige powerfactor, die veel kleiner is dan 1, zorgt ervoor dat er grotere stromen lopen dan dat het strikt noodzakelijk was voor het afgeleverde netto vermogen, en deze grotere stromen zorgen nu voor meer verlies in de leidingen van het aanvoernet.
Lage PF betekent hogere verliezen in het aanvoernet
Hogere stromen zorgen ook voor grotere spanningsval in het aanvoernet, wat betekent dat de spanning zoals die binnenkomt bij de eindverbruiker lager is. Dit is ongunstig voor bijvoorbeeld lampen, die minder sterk branden.
Lage PF betekent een hogere spanningsval in het aanvoernet
Deze hogere stromen moeten echter wel geleverd worden, en daarvoor zijn wel grotere generatoren nodig (aan de generatiekant van het net) dan wanneer ik geen R-stromen had gehad.
Lage PF betekent ook grotere generatoren voor het genereren van de hogere stroom
Wanneer je als gebruiker een aftap hebt van 1 x 35 A, maar je PF is maar 0,5, dan haal je maar de helft aan het netto vermogen uit je aftap. Want 1 x 35 A bij 230 V zou maximaal een vermogen van 230 V * 35 A = 8050 W zijn. Maar wanneer je PF 0,5 is, dan geldt dat Is = 35 A en Ip = 17,5 A, dus je haalt maar 4025 W uit je aftap. Wil je meer, dan moet je of je PF corrigeren of een grotere aftap huren en dus meer betalen.
Lage PF betekent dat je minder netto vermogen uit je aftap kunt halen
De verliezen agv hogere stromen binnenshuis van een eindverbruiker zijn niet zo groot, omdat de lengte van de leidingen niet zo lang zijn. Maar het feit dat er hogere stromen lopen, betekent ook dat de verbruikers zelf, en de componenten die met deze hogere stromen te maken krijgen, wat de levensduur van deze componenten verkort.
Lage PF betekent hogere stromen en meer belasting voor de componenten, dus een kortere levensduur




62 reacties op “De powerfactor uitgelegd”
Een slechte PF kan ook worden opgevangen door het plaatsen condensatoren parallel aan de verbruiker – tenminste, als de slechte PF wordt veroorzaakt door een spoel zoals een te kleine transformator.
Ook kan een verbruiker met een capacitieve belasting een met een inductieve belasting compenseren.
Maar veel belastingen met slechte PF zijn niet-lineair, en die zijn niet zo makkelijk te compenseren
Want to replace all my garden PL-7 ’s (PF 0,34 inductive) by the “non balast” type eg Philips Eco Lustre 7w.
Not a word is found about the PF of these or other “non balast” type enery saving lights.
Is it “1” or is is capacitive ?
Apreciate your answer.
dear Martin,
The compac fluorescent lamps consist of a tube with a plasma and from there generate light. They need a form of current limiter which normally is a coil, so inductive. Now with the electronic ballasts operating a high frequencies, one can also use a capacitor, or one can rectify the incoming grid voltage and work from this rectified voltage by using switches. In such case the total is not anymore inductive or capacitive. But as the current drawn from the grid is not sinusoidal, the power factor is still less than one. So basically for an electronic ballast, which is build into the lamp, I cannot say for sure.
Why do you need to know whether it is inductive or capacitive?
Als mijn apparaat een lage powerfactor heeft, lopen er dus grote stromen door. Als dat door een printplaat of kleine elco’s moet, dan heeft dat toch ook een zekere warmte-ontwikkeling ten gevolge?
Is dat inderdaad zo, en wie betaalt die warmteontwikkeling dan?
Gr.M.
@ Mark,
Klopt, er is warmteontwikkeling binnen jouw huisleidingennet agv de blindstromen opgewekt door jouw verbruikers.
De blindstromen door het totale net zijn wellicht veel groter omdat dan alle blindstromen van ieder huishouden bij elkaar worden opgeteld, en deze blindstromen lopen door het totale netwerk heen.
Jij betaalt voor jouw verliezen in je eigen huisleidingen net. Deze zijn overigens klein.
Soms denk ik deze theorie onder de knie te hebben.
Heb ik goed begrepen dat warmteverliezen door blindstromen niet genoteerd worden door de teller?
Is het dan mogelijk een electrische verwarming te ontwerpen met een héél ‘slechte’ powerfactor en zo de electriciteitsleverancier in het zak te zetten (maar ook het milieu) ? Ik vraag me dit af naar aanleiding van een commerciele reactie op de topic ‘hoe onzuinig is elec. vloerverwarming’.
Of heb ik het helemaal niet begrepen en maak ik me onnodig ongerust?
Hoi Willy,
Alle werkelijke opgenomen vermogen zul je moeten betalen. Wanneer je kijkt naar warmteverliezen agv blindstromen, dan zul je die ook betalen. De blindstoom zelf, is een stroom die niet gelijk loopt met de spanning, en daardoor wordt er geen netto vermogen (P = U x I) afgenomen. Er wordt wel vermogen heen en weer gepompt, waardoor het netto effect nul is.
Nu deze blindstroom zorgt ervoor dat er verlies is over de kabels, en dit verlies is werkelijk afgegeven vermogen. Dus, voor dit verlies, moet je stellen dat daar spanning (U_verlies) en stroom (I_blind) weer wèl gelijk oplopen, er gewoon vermogen wordt afgegeven en waarvoor betaald moet worden.
Dus, je hebt nu op twee manieren vermogen die overgedragen wordt. De U_net is de netspanning. Daaruit volgt een I_schijnbaar, die uit een actieve component bestaat (I_actief) die gelijk oploopt met U_net en waardoor er dus werkelijk netto opgenomen vermogen is (noemen we P = U_net x I_actief). Verder bestaat I_schijnbaar ook uit I_blind, en deze loopt zodanig uit fase met U_net dat er steeds vermogen heen en weer wordt gepompt, dus netto resultaat nul. Maar, deze I_blind zorgt wèl voor een spanningsval (U_verlies) over de kabels, en dus is er wel netto vermogensafdracht door I_blind x U_verlies.
Voor het gedeelte aan leidingen in jouw huis, geldt dat U_verlies klein zal zijn, en dus zal je daar niet veel van merken. Echter voor het netbedrijf, die alle blindstromen tezamen te zien krijgt, kan het significant zijn. Daarbij geldt nu dat bedrijven wel belast worden voor afgenomen blindvermogen (extra meter) en huishoudens niet. De kosten van een extra meter zullen denk ik niet opwegen tegen de extra inkomsten voor het netbedrijf bij huishoudens.
@mvdsteen:
Hoi, dank voor je uitleg!
Ik snap dat er kleine verliezen zijn in het huisleidingennet tgv blindstroom. Deze zullen niet veel te betekenen hebben, omdat deze geleiders niet veel weerstand hebben.
Maar ik vraag me het volgende nog af:
De blindstroom loopt ook door de blindstroom-verwekker. Kan de blindstroom daar nog warmteverliezen veroorzaken, of is het dan per definitie geen blindstroom meer? Stel dat dat een LED-lamp is met een printje die de spanning van 220V naar 5V of 12V brengt. Als die lamp een PF heeft van 0.5, dan loopt er toch een (voor die lamp) aanzienlijk vermogen doorheen, qua blindstroom. Merk je daar nog wat van wat betreft warmteontwikkeling? Het gaat immers ook door de lamp en alle componentjes met bijbehorende weerstanden en rendenmenten. Heeft de lamp op die manier een verbruik waar je wel (ohms verbruik) en niet (rendement op blindvermogen) voor betaalt?
Groet,
M.
@willy
Dat schijnt in theorie te kunnen ja.
Ik had eens een docent toegepaste elektriciteit, die sterke verhalen had over de tweede wereldoorlog. Er waren toen slimmerikken die de Duitsers beduvelden met een dergelijke truc. Er was toen immers een rantsoen op electriciteit, maar de meters toen noteerden geen blindstroom…dus werd er naar hartelust aan de cos phi gesleuteld om zo toch extra vermogen te kunnen nemen.
Ik denk dat dat feest tegenwoordig niet meer door zal gaan.
Hoe kun je de blindstroom van een gegeven apparaat wijzigen dan? Als dat eenvoudig mogelijk is zouden mensen dat nu toch ook wel op grote schaal doen?
@mvdsteen
Bedankt voor je uitleg, doch ben ik noch niet zeker het goed te begrijpen. Dat er door blindstroom werkelijk vermogen opgenomen wordt is wel duidelijk (bewijs is warmteafgifte) maar hoe gaat de teller dat registreren? En met de opmerking van Mark over het beduvelen van duitsers ben ik zekers de weg weer kwijt.
Ben mecanieker en moest een paar jaar geleden ergens een inpakmachine gaan installeren. Bij het opstarten sprongen de zekeringen. Bleek ergens binnenin een grote transfo te zitten die verkeerd aangesloten zat (ik begreep absoluut niets van het schema ). Komt een electrieker en die sluit de motor gewoon aan (zónder de transfo) tussen twee fasen, en klaar was kees.
Wat deed die transfo dan daar ? Voorzover ik me herriner was het de bedoeling de motor óver de transfo tussen fase en nulleiding te koppelen (maar daar ben ik nu niet echt zeker meer van, zoals gezegd begreep ik het schema niet). (De machine werdt gebouwd vóór de oorlog, de transfo was niet origineel, misschien was dit zo een soort truc waar Mark over spreekt.)
Ik begrijp zelf niks (meer) van de truc, slechts het verhaal is blijven hangen. Op de een of andere manier wist men in elk geval een met kleine cos phi afgenomen stroom binnenshuis effectief te gebruiken…
@Willy
Een wat populaire uitleg.
De wisselspanning van het lichtnet heeft een sinusvorm. Bij een normale (ohmse) belasting volgt de stroom exact de spanning. Sluit je een spoel (zelfinductie) aan op het lichtnet dan kan de stroom de spanning niet volgen. Deze ijlt na. In theorie loopt de stroom 90 graden achter op de spanning. Het door de spoel opgenomen vermogen (V x I cosinus 90) is dan nul, want de powerfactor = cos 90 graden = nul.
Er loopt echter wel stroom. Dat is pure blindstroom.
Sluit je een condensator aan dan loopt de stroom voor de spanning uit. Deze ijlt dan 90 graden voor. De hoek phi is dan -90 graden en het opgenomen vermogen is dan: V x I x cos -90 = 0.
Er loopt hier ook (blind)stroom.
Als je nu zowel een spoel aan het lichtnet aansluit en een condensator met een gelijke impedantie (=wisselstroomweerstand) wordt het naijlen van de stroom volledig gecompenseerd door de condensator. Er loopt dan effectief geen stroom via het lichtnet en er is dus ook geen blindstroom.
In de praktijk tref je veel situaties aan (zoals bij een motor) met een menging van ohmse en inductieve belastingen. De naijling van de stroom is dan veel minder dan 90 graden, maar b.v. 25 graden. De Powerfactor is dan cosinus 25 graden = 0,91.
Er loopt dus ook blindstroom. Deze is te compenseren m.b.v. een specifieke condensator. Dit verandert niets aan het door de motor opgenomen vermogen. Je helpt hierbij alleen de netbeheerder, want de geleverde blindstroom wordt volledig door de condensator gecompenseerd.
@Arie
Bedankt om het nog allemaal eens grondig uit te leggen.
Maar de vraag was eigenlijk: Is het mogelijk om een met kleine cos phi afgenomen stroom binnenshuis effectief te gebruiken, zoals die docent van Mark beweerde?
Als ik het artikel hierboven goed begrijp: dus niet.
Toch heb ik ooit elders dergelijke verhalen uit de oorlog nog gehoord.
Mogen we deze verhalen dan definitief afdoen als nonsens?
@ Mark, @ Willy,
Het zou toch mooi zijn, wanneer we de blindstroom gebruiken voor het genereren van warmte waarvoor we dan vervolgens niet betalen. Volgens mij is het nonsense.
De blindstoom is dat gedeelte van de schijnbare stroom die niet in fase loopt met de originele aangelegde spanning (in mijn eerdere verhaal I_blind loopt niet in fase met U_net). Maar deze I_blind creëert wel een vermogensverlies over de weerstand in alle leidingen, dus wat gebeurt er dan?
Mijn uitleg zou de volgende zijn: doordat de blindstroom I_blind door de leidingen loopt, veroorzaakt deze blindstroom een spanning over de weerstand van deze leidingen (U_verlies). Nu geldt echter wel dat I_blind in fase loopt met U_verlies, dus wordt er netto vermogen gedissipeerd. En wat zie ik dan aan de netkant? Dat deze spanning U_verlies wordt opgeteld bij de U_net! Dus, agv het lopen van I_blind door de weerstand van de leidingen, wordt er een U_verlies gecreëerd die in fase is met I_blind en die wordt opgeteld bij U_net! Dus, de netspanning wordt iets beïnvloed agv de U_verlies. Of, je mag het ook zien als dat de cos phi iets verandert waardoor er weer meer vermogen wordt opgenomen!
Dit klinkt misschien raar. Laten we eens naar een zuivere condensator als belasting. Dan geldt dat cos phi = cos -90 = 0.
Nu voeg ik er in serie een kleine weerstand aan toe, zo klein dat het de stroom nauwelijks beïnvloedt, waar dus het gros van de blindstroom doorheen loopt. Hierdoor zal phi toenemen, en dus de cos phi groter worden, stel 0,2. In dat geval heb ik dus ineens wel verlies, en dat terwijl al het verlies afkomstig is van de warmteontwikkeling in de weerstand, gecreëerd door de blindstroom.
Stel ik maak mijn weerstand een stuk groter, stel net zo groot kwa weerstand als dat de impedantie van de condensator is. Dan volgt dat de stroom die loopt, een grootte heeft die in relatie staat met de wortel uit de som van de kwadraten van de Ohmse weerstand en de weerstand van de condensator. En de cos phi is inmiddels cos -45 = 0.7.
@Willy
Je kunt nooit meer energie uit het net halen dan dat je meter registreert. Ook met een lagere powerfactor (cos phi) is dat niet mogelijk. Een apparaat dat veel blindstroom veroorzaakt profiteert ook niet, immers de spoelen of condensatoren hierin nemen geen vermogen op.
Hoe dat in de oorlog is gegaan weet ik niet, maar als er toen geen meters waren met een cos-phi correctie, zou er meer energie worden geregistreerd dan dat er werkelijk werd gebruikt. Dat pakt dan ongunstig uit.
Bij blindstroom loopt er wel extra stroom in de netleidingen, die voor de meter een huis binnenkomen, maar daaraan kun je legaal geen extra energie onttrekken.
Mark asked: “Kan de blindstroom daar nog warmteverliezen veroorzaken, of is het dan per definitie geen blindstroom meer?”
OK, uit bovenstaande opmerkingen van Arie en Mvdsteen concludeer ik dus dat blindstroom per definitie nooit vermogen levert. De cos phi “stelt zich in” naar al hetgeen het onderweg tegenkomt (zoals de weerstand na de condensator van mvdsteen). En blijft daarbij dus altijd neutraal bij het leveren van vermogen.
Dank 🙂
Klopt Mark. Blindstroom levert per definitie geen vermogen. Als je dus een belasting creëert met alleen een condensator, dan heb je alleen maar blindstroom. Op het moment je meer weerstand toevoegt, dan creëer je dus meer actieve stroom en gaat je cos phi meer naar 1 toe.
Oke, ik snap het hele blindstroomverhaal maar half, ben dan ook geen electricien. Ik heb dit verhaal doorgeworsteld omdat ik voor mezelf een beeld probeer te vormen over de Pharox LED-lamp. Meer precies: hoe duurzaam is hij nou ten opzichte van andere spaarlampen? Ik heb er jammer genoeg nog geen in het echt kunnen aanschouwen, dus als je een kwalitatief oordeel kunt geven over hoe fijn de lamp is, dan ben ik daar zeer in geïnteresseerd. Tot slot: stel dat de Pharox op grote schaal gebruikt zou gaan worden, wat voor effect heeft dat blinde vermogen dan op het electriciteitsnet?
Hoi Paulus,
De duurzaamheid van een lamp hangt van een aantal factoren af:
Voor item 1, geldt dat de hoeveelheid opgenomen stroom en de gebruikte grondstoffen omgerekend kunnen worden in een aantal kWh of wellicht een aantal uitgestoten CO2 in de lucht. De levensduur speelt een belangrijke rol; hoe langer de lamp meegaat, des te minder vaak deze moet worden vervangen en dus kan productie uitgespaard worden; stel ik vergelijk een gloeilamp (1000 uur) met een thermisch goed gedesignde ledlamp (50.000 uur). Dan kan ik de productieenergie afschrijven over 50.000 uur bij de ledlamp. Wanneer de ledlamp 10x meer energie kost voor productie als de gloeilamp, dan is de ledlamp over zijn levensduur nog altijd 5x minder belastend.
Dit kan ook voor item 2, namelijk het verbruik over de levensduur omrekenen in kWh of CO2. De efficientie van een lamp is hierbij een belangrijke factor, hoe hoger des te beter.
Item 3 wordt vaak niet meegenomen, maar is ook belangrijk. Bij papier zie je dat; er wordt vaak gebruik gemaakt van oud papier om nieuw papier te maken. Je zet dan de besparingen bij grondstoffen bij productie af tegen het ophalen en verwerken van oud papier.
Ik weet niet te zeggen in hoeverre het productieproces van de Pharox milieuvriendelijk is of niet. Ik weet wel dat deze vernuftig in elkaar gezet is, wat bij productie helpt om geen fouten te maken. In hoeverre deze lamp een lange levensduur heeft, weet ik ook niet. Dus voor punt 1 kan ik niets zeggen.
Voor punt 2 weet ik dat de efficiëntie 30 lm/Watt is. Er zijn inmiddels betere, dat wil zeggen ledlampen met een hogere efficiëntie en ook met warmwit licht. Kijk daarvoor op mijn lampoverzicht. Voor punt 2 ook van belang is de powerfactor. Deze is slecht bji de Pharox. Er is voor 4 W vermogen maar liefst 75 VA aan schijnvermogen. Dat wil zeggen dat er relatief grote stromen lopen om deze kleine 4 W aan netto vermogen te realiseren. Deze grote schijnbare stroom (bestaat uit blindstroom en een klein beetje uit de stroom die zorgt voor het netto vermogen) zorgt voor extra belasting van de netwerken waardoorheen de stroom moet. Ik kan niet zeggen hoeveel dat extra kost in het gebruik van 1 lamp. Het zal wel meevallen over de 4 W die de lamp zelf opneemt, misschien zelfs nog minder dan 5 % daarvan. Bij grote schaaltoepassing zal men echter eerder aan limieten van het net (of van de stop) komen, dit omdat de stromen snel groter worden, terwijl men niet echt nuttig gebruik maakt van deze grote stromen (het grootste gedeelte van de afgenomen stroom is dan heen- en weer aan het lopen over het net, zonder echt energie over te brengen naar de eindverbruiker.
Marcel,
Ik heb een vraag betreffende de PF.
Stel ik heb een systeem met een verbruik van bv. 100W met een PF van 0.80
Ik verminder het energie verbruik van het systeem met 10% naar 90W.
Echter het resultaat is ook een power faktor daling van 10% naar 0.72.
Ik bespaar dus 10% opgenomen vermogen, echter wat is het effect op het totale verbruik, reëel en blindvermogen.
Besparen we nu energie of wordt mijn besparing teniet gedaan door het extra blindvermogen wat de centrale moet gaan leveren.
Ik heb geen idee hoeveel watts de energie maatschappij kwijt is aan het heen en weer pompen van de blindstroom, ik weet nl. niet wat de leidingverliezen in watts zijn.
Ik ken nl. de Rnet niet.
Heb jij een idee hoe dit zit.
Bij voorbaat dank voor je reactie.
met vr. groeten,
Dick van Riel
Dick, als consument (dus niet als bedrijf) betaal jij geen blindstroom, dus alles waarmee je je vermogen P (in Watt) kunt verkleinen bespaar je.
Je voorbeelden:
Situatie 1: P = 100 W, PF = 0.8
Situatie 2: P = 90 W, PF = 0.72
Consument: betaalt alleen P, dus bespaart 10 % op de elektriciteitskosten.
Bedrijf: betaalt naast P ook blindvermogen. Ik weet even niet hoeveel deze daarvoor betaald, als jij een bedrijf bent kijk dan even op je afrekening.
Nu bereken we het blindvermogen R in VA. Dit gaat als volgt:
P/S = PF, dus S = P/PF
S^2 = P^2 + R^2, dus R = sqrt(S^2 – P^2) = sqrt (P^2/PF^2 – P^2) = P*sqrt( (1/PF^2 – 1 )
Nu volgt voor situatie 1:
P = 100 W, PF = 0.8, R = 100*sqrt(1/0.8/0.8 – 1) = 75 VA.
Nu volgt voor situatie 2:
P = 90 W, PF = 0.72, R = 100*sqrt(1/0.72/0.72 – 1) = 96 VA.
Dus je ziet dat de toename van R 28 % is en dus meer dan de afname van P. Nu hangt het van de te betalen prijs af voor kVAh of het gunstiger is financieel.
R = sqrt(S^2 – P^2)
Marcel,
Bedankt voor je uitleg.
Even afgezien van de financiële aspecten, mijn besparing in energie (10%)wordt dus meer dan teniet gedaan door het extra te leveren blindvermogen van 28%, correct ?
Hoi Dick,
Je bespaart dus 10 % in energie (omdat je vermogen 10 % lager is). Verder is er een 28 % groter blindvermogen. Echter, dit blindvermogen gaat heen en weer tussen jouw applicatie en het netwerk. Het is dus niet direct energieverlies.
Het verlies zit hem in andere zaken, namelijk er is stroom nodig om ook het blindvermogen heen en weer te transporteren, wat de totaal stroom (wortel uit kwadratische som van stroom voor echt vermogen en stroom voor blind vermogen) groter maakt. De gebruikte transformatoren in transformatorhuisjes, de gebruikte kabels etc moeten nu groter gedimensioneerd worden dan dat strikt noodzakelijk zou zijn geweest voor alleen het netto vermogen zelf. Deze overdimensionering moet steeds meer worden naarmate meer en meer blindvermogen wordt afgenomen.
Het is dan eigenlijk zonde, want het gaat de verbruiker om de echte energie (gekoppeld aan vermogen P) en niet zozeer om de energie die heen en weer fietst (het blindvermogen R). Heb je nu belastingen of verbruikers die vor 100 W aan vermogen ook 1000 VAr aan blindvermogen nodig hebben, dan is het totaal vermogen 1410 VA en dat is dus meer dan waar het eigenlijk om gaat. En omdat er een totaal vermogen van 1410 VA door het net moet worden getransporteerd, moeten de trafo’s en bekabeling en zekeringen daar wel op aangepast zijn.
Als je verder vragen hebt hoor ik het wel.
Marcel,
Bedankt voor je snelle reactie.
Als ik het goed begrijp zijn de reëele extra verliezen een resultaat van de grotere blindstoom.
Deze extra verleizen zijn dan delta I^2*Rnet.
Enig idee waar je in grootte aan moet denken voor de ohmse weerstand R van een netwerk ?
Met vriendelijke groeten,
Dick van Riel
Dick,
De extra verliezen zitten hem in het feit dat de stroom groter is dan strikt noodzakelijk. En dus het extra vermogensverlies is dan (stroom_totaal – stroom_nettovermogen) * R_net. Ik ken helaas R_net niet, maar die zal zeker laag zijn, in de orde van minder dan 1 Ohm is mijn inschatting.
Verder denk ik dat de kosten die gemoeid zijn met het aanschaffen van grotere dan strikt voor het netto vermogen noodzakelijke transformatoren hoger zijn dan de kosten voor het extra verbruik agv R_net.
Marcel,
Bedankt voor je hulp.
Met vriendelijke groeten,
Dick van Riel.
Hallo,
Allaereerst de complimenten voor de lampmetingen, ze zijn zorgvuldig en geven mij veel gegevens die ik voor de professionele toepassing nodig heb, echter….
Is het mogelijk naast gegevens over de power factor bij metingen ook gegevens ten aanzien van de gegenereerde hogere harmonischen te publiceren?
Immers formeel is power factor gedefinieerd als :
p.f. = som harmonischen (P)/ som harmonischen (S)
Hierin wordt dus het deel van S en P wat door hogere harmonischen wordt gegenereerd meegenomen.
In bovenstaande verklaring en het commentaar wordt alleen gesproken over de grond harmonische (hier in NL 50Hz) en alleen in zon geval is cos-phi gelijk aan de power factor.
Waarschijnlijk worden de metingen wel op de juist manier gedaan en is het resultaat van die meting inderdaad de power factor (true RMS meting). Ik ben dus aanvullend daarop geïnteresseerd in een frequentie spectrum waaruit kan worden afgelezen welke hogere harmonischen in welke mate worden gegenereerd (frequentie-vermogens spectrum).
Het aandeel en de verdeling van hogere harmonischen is voor mij belangrijk voor de dimensionering van professioneel gebruikte verlichtingssystemen (net als het aanwezig zijn van een lage cos phi of power factor). Op huisaansluiting niveau is voor de thuis gebruiker (zoals in voorgaande commentaren aangegeven) niet belangrijk. Echter in grote installaties moet een minimum cos-phi en een maximum aandeel hogere harmonischen worden gehaald.
Het toepassen van LED verlichting met een lage cos-phi (of p.f.) en veel hogere harmonischen betekend dus dat er aan de verbruikerskant extra maatregelen in de vorm van cos-phi verbetering en/of filtering moet worden opgenomen. Deze maatregelen kosten geld en maken dus de toepassing van LED verlichting professioneel minder aantrekkelijk.
Groeten
Bas van Duijnhoven
Royal Haskoning
Hoi Bas,
Eerst mat ik met de HAMEG 8115-2, en die heeft een bandbreedtelimiet van 400 Hz, dat is dus niet voldoende voor sommige lampen waar PF correctie wordt toegepast en ook voor lampen met wat intelligente elektronica die piekige stroomvormen afnemen. Echter hield de HAMEG wel rekening met hogere harmonischen, alleen kon de hogere frequenties hiet goed meten.
Daarom heb ik sinds kost een simpele maar doeltreffende meting, nl datasamples meten over een weerstand voor de stroom te bepalen. En dat doe ik met 10.000 Hz. Daarmee kan ik meerdere harmonischen bepalen. Ik zal eens kijken of ik bij de nieuwe metingen die ik ga publiceren standaard een grafiek plaats met de harmonic content van de stroom die door de lamp loopt. Houdt dan de nieuwe lampmetingen in de gaten.
Marcel,
Bedankt voor de snelle reactie. Ik ga met belangstelling de komende lamp metingen in de gaten houden.
Ik zie met verbazing en verbijstering de soms absurd lage power factors van een aantal LED lampen. Dat gecombineerd met de soms hele vreemde stroom vormen met enorme hoeveelheden hogere harmonischen maakt dat mijn conclusie is dat LED technologie voor professionele toepassingen (kantoor gebouwen enz) zeker nog niet volwassen is.
Naar mijn mening moet er nog flink ontwikkeld moet worden om de omvormers voor de LED’s op een elektrotechnisch acceptabel niveau te krijgen. Power factors van 0,9 of hoger en een harmonische vervorming van enkele procenten zijn naar mijn idee vaak nog ver weg.
Dit is jammer aangezien in de professionele markt toch steeds vaker gevraagd wordt naar LED verlichting als alternatief voor de traditionele TL verlichting. Wij moeten daarop vaak nog negatief adviseren gezien de totale kosten over de levensduur van de aan te brengen verlichting.
Bij deze een oproep aan fabrikanten om te werken aan hoge power factoren en een lage harmonische vervorming van de LED lichtbronnen. Dit zal de acceptatie in de professionele markt flink versnellen.
Groeten
Bas van Duijnhoven
Royal Haskoning
Hoi Bas,
Zie dit artikel van de Viva Lite. Daar heb ik een grafiek toegevoegd die de harmonischen weergeeft van de stroom door de lamp heen.
Hoi Bas,
Ik zal er binnenkort een logarithmische y-schaal van maken, dan kun je beter de hogere harmonischen zien (nu met een lineaire schaal zijn ze snel uit beeld).
Je zou (dit is een suggestie) de x-as kunnen verdelen in veelvouden van de grondharmonische dus (2,3,4,5,6,7,8,9 enz.)
en de Y-as in percentage van de totale stroom.
op deze wijze heb je vast x en y assen.
Over het algemeen komen harmonischen boven de 15 (750Hz) niet voor, dus wat mij betreft hoef je daarboven geen waarden weer te geven. In dat geval is een logarithmische schaal niet nodig.
Ow bijna vergeten:
Hardstikke bedankt!!!
Hoi Bas,
Update is verwerkt. Nu in % op een logaritmische schaal. Ik vind het wel mooi zo. Ik heb nog wat metingen in backlog, waar ik niet van overal de stroomvormen heb. Deze metingen die ik alsnog publiceer binnenkort, daarvan heb ik dan niet dit stroomprofiel. Maar alle metingen die ik nu doe, zullen dit stroomprofiel hebben.
Marcel geweldig, bedankt!!!
Heeft de blindstroom effect op spannings-automaten bij inschakelen?
Jullie praten allemaal over power factor. Is dit hetzelfde als de cos phi??
AvdB, powerfactor (PF) is completer dan alleen cos_phi. In cos_phi zit alleen het faseverschil tussen spanning en stroom. In PF zit daarnaast ook de mate van ongelijkvormigheid. Dus ik kan een sinusvormige spanning en een blokvormige stroom hebben die in fase lopen, dqn is cos_phi = 1 echter PF zal kleiner zijn dan 1.
Wel eens gehoord van een ‘conjugate match’?
Als de belastings-impedantie de “complex geconjugeerde” is van de bron-impedantie, dan vindt er maximale vermogens (energie) overdracht plaats tussen de energie bron en de belasting.
Aangezien de impedantie van het lichtnet (als bron) vrijwel geen ‘imaginair’ impedantie gedeelte heeft (de stroom ijlt niet na op de spanning, en andersom), moet ook de belasting impedantie een reele weerstand zijn (geen impedantie met capacitief of inductief gedeelte) om een optimale vermogen-overdracht te realiseren.
Door veel ‘blind vermogen’ (oftewel imaginaire belastings- impedantie) kan het het lichtnet als bron vervuilen, (heeft geen zuiver reele impedantie waarde), zodat de stroom na/voor gaat ijlen op de spanning.
Bijvoorbeeld, door grote industriele electro motoren krijg je lichtnet vervuiling (inductieve belasting). Hierdoor is het opgenomen vermogen van zuiver reele belastings-impedanties niet meer optimaal.
Om die reden is het belangrijk om een powerfactor=1 na te streven in lichtnet belastingen. Grote electromotoren op het lichtnet moeten uitgerust worden met grote condensatoren. Iets dergelijks doet ook de LED-driver van Lioris http://www.lioris.nl/products.aspx?id=292 .
Ik heb gemerkt dat zelfs veel HTS-ers electro weinig begrijpen van blind vermogen.
Complimenten voor mvdsteen en Arie G die een heldere uitleg geven m.b.t. voor- of naijlen stroomcomponenten.
Een ideale spoel of condensator worden niet warm en toch loopt er stroom door de draden van leverancier tot gebruiker.
De netwerkverliezen zijn voor alle stroom mischien 15% dus de leverancier is niet blij met blind vermogen.
De gebruiker thuis betaald er niet want de bedrading thuis wordt echt niet warm van zo’n beetje stroom.
Echter ook voor de leverancier van het wel mee: Sommige apparaten zijn meer ‘capacitief’ (spaarlampen/leds?) terwijl andere apparaten meer ‘inductief’ (trafo’s in audio) zijn wat elkaar in een woonwijk wat compenseert.
Het zou me niet verbazen dat de spaar en LED lampen het blind vermogen compenseren van mijn audioversterker of TV.
Niet lineariteit is een groter probleem: Allerlei geschakelde voeding vervuilen het netwerk met hoge frequentiecomponenten tot gevolg. Vreemd dat dit bij die weinig verbruikende lampen nu ineens een issue is. Elke TV heeft een geschakelde voeding en verbruikt toch echt een stuk meer. De goedkope electronica in zo’n lamp zal er zeker mee te maken hebben.
In een kantoortuin met tientallen lichtbalken (met elk weer vele tientallen leds) met slechte voedingen die allemaal dezelfde storende eigenschappen hebben is dit natuurlijk wel een probleem.
Nog een vraag aan Bas n.a.v. bericht 33. Wij waren van plan ons magazijn uit te rusten met Led TL’s. Daarop gaf onze eigen technische man (onder verwijzing naar jou artikel)aan dat er nog verder ontwikkelt moet worden om de Power factors van 0,9 of hoger te bereiken. Daarop deze site als niet Electro man “doorgeworsteld”. Blijf dan toch met een praktische vraag zitten. Je stelt: Wij moeten daarop vaak nog negatief adviseren gezien de totale kosten over de levensduur van de aan te brengen verlichting” Stel je hebt PF van zeg boven de 0,8 en de prijs t.o.v. besparing energieverbruik is goed. Is het dan verkeerd geredeneerd om nu toch te vervangen?. Immers, zolang je wacht loopt de energiemeter door. Vraag is dan of wachten op een betere versie (die er natuurlijk wel moet komen) vanuit praktisch oogpunt juist is. Stel je verdient de investering terug op 3 jaar. Dan kun je t.z.t. toch altijd weer bezien wat je doet.
Gaat mij dus niet om bepaald artikel, maar om de gedachtegang. Hoe sneller minder energieverbruik, dus duurzaam is dan toch winst?
Ik heb een vraag over de power factor en harmonische.
Ik heb me flink verdiept in de powerfactor en harmonische kwestie en weet er best veel vanaf nu.
Het punt is alleen waar ligt de grens of wanneer kunnen er storingen verwacht worden door harmonische?
Stel dat ik 400 halogeenlampen met een pf van 1 vervang door 400 zuinige led spots met een pf van 0.93 en de derde harmonische is 10% van de eerste (eigenlijk 4 % teveel, maar de andere harmonischen zijn goed). Kunnen er dan problemen verwacht worden (qua storing van apparatuur) of is dit alleen het geval bij led spots met een pf van 0,5 en meerdere harmonischen boven het toegestane percentage van de eerste?
@Frank:
Of er problemen optreden is grotendeels afhankelijk van de hoeveelheid normaal vermogen wat in bedrijf is tov het LED vermogen. Ik kan daar dus geen antwoord opgeven zonder de specifieke situatie te kennen.
Feit is wel dat de energie bedrijven eigenlijk niet monitoren op harmonischen of slechte powerfactors op de aansluiting. Als je een meter hebt zonder powerfactor registratie zeg ik vervangen.
Mocht je een meter hebben met powerfactor meting is het een beetja afhankelijk wat de verlaging is, ik verwacht niet al te veel problemen.
@Ruben:
De 3e harmonische is een beetje bijzonder in de zin dat 3e harmonische stromen in het nul punt van een 3-fasen installatie elkaar niet opheffen, maar juist bij elkaar worden opgetelt. Dit resulteert in een 3e harmonische stroom in de nul van ca 30% van de fase geleiders. Afhankelijk van de wijze waarop de kabel berekend is zou deze overbelast kunnen worden. De praktijk is dat hier veelal voldoende reserve aanwezig is en er geen defecten zullen optreden.
De grens van toegestane harmonischen is vastgelegd in NEN-EN-IEC 61000-3-2. Of er storingen in andere apparatuur optreden is afhankelijk van de mate van verstoring door de nieuwe LED lampen en de gevoeligheid voor storingen van de overige apparatuur die verstoord kan worden. Hierover kan je dus zo snel niets zinnigs zeggen. Feit is wel dat indien de LED lampen onder de waarden in de bovengenoemde norm blijven en de overige apparatuur voldoet aan de volledige NEN-EN-IEC 61000 serie er, als het goed is, geen problemen optreden. Er is dan sprake van elektromagnetische compatibiliteit (EMC).
Verder zal Marcel binnenkort een extra artikel plaatsen over harmonischen en THD in de metingen. Meer info volgt dus.
Groeten
Bas
Boze tongen beweren dat de slimme energiemeters, zoals van OXXIO óók de blindstroom meten en in rekening brengen.
Wie kan hier meer over vertellen?
Groeten Johan
Jammer dat er nog geen antwoord is op de vraag van Johan Krabbe.
Deze vraag is nu zeer relevant!
Overigens is (m.i.) niet de blindstroom het grote probleem bij LED en CFL lampen, maar de golfvorm. Mooi dat die tegenwoordig in de testrapporten staat. Jammer dat in die grafieken niet de maximaal toegestane waarde van de harmonischen getoond wordt, omdat het vermogen van de lamp te laag zou zijn. Maar bij 10-30 lampen per huis (ze geven erg weinig licht) of bij duizenden lampen in een gebouw doen die maxima er wel toe. Ik zou wel eens informatie willen hebben over de problemen die dit kan geven in de wijktransformatoren. Problemen met EMC verwacht ik niet omdat het per lamp om kleine stroompjes gaat en de lange voedingsleidingen voldoende zelfinductie hebben om de hogere harmonischen te dempen.
n.a.v. bericht 41 (Piet): deze HTS’er snapt wel hoe het zit met blind vermogen. Zowel voor als na de meter zorgt deze stroom voor ohmse verliezen (warmte). Die zijn gering maar ongewenst. Erger is het dat de leverancier zijn transformator(stations) moet bouwen voor een maximale stroom en als die stroom een slechte power factor heeft kan die trafo minder vermogen leveren aan de klanten. De netwerkbeheerder moet dus zwaardere transformators plaatsen (bijvoorbeeld 120 kVA om 100 kW te leveren) en dat kost extra.
De maximaal toegestane limieten voor verlichtingssystemen vanaf 25 W is wel te vinden, zie de grafiek van een lamp met P > 25 W in dit artikel. Die kun je dus, als je wilt, ook gebruiken voor verlichting van < 25 W per stuk.
Mbt opmerking "problemen met EMC …. voldoende zelfinductie": ik meet de stroom die vanuit het net naar de lamp gaat. Alle harmonischen bepaal ik van die stroom. Die harmonischen lopen echt. Wellicht dat ze niet meer lopen door de kabels die van het wijktransformatorhuisje komen echter dan is dan lijkt mij niet vanwege de zelfinductie van de kabels tussen huishoudens en het wijktransformatorhuisje. Maar vanwege het uitmiddelen van deze ene lampstroom op de vele stromen die gevraagd worden door andere apparatuur in hetzelfde huishouden en tevens over meerdere huishoudens verdeeld.
Hoewel dit alweer een erg oud topic is heb ik er een paar vragen over.
Stel ik heb twee apparaten:
1) P = 700W PF = 0,7
2) P = 500W PF = 0,5
Als ik het verhaal goed begrijp is er voor beide apparaten 1000VA nodig om ze te laten werken. Voor apparaat 2 betaal ik als consument het minste aan mijn energie rekening.
Stel dat dit de enige twee apparaten zijn die worden aangesloten op een energie centrale, bij welk apparaat wordt dan het minste CO2 uitgestoten?
Alvast dank voor je reactie.
Gr. Willem
Hoi Willem,
Per kWh (= P) aan gegenereerde energie is er een bepaalde CO2 uitstoot mee verbonden. Echter per kVAr (= R) aan blinde energie is er wellicht ook een CO2 uitstoot mee gemoeid, alleen die waarde ken ik niet. Als ik die waarde niet ken, dan kan ik ook geen vergelijk maken tussen de ene verbruiker met een hoeveelheid aan P en R en de andere verbruiker met een andere hoeveelheid P en R.
Beste Marcel,
Dank voor je antwoord. Ik zal eens kijken of ik deze gegevens bij een energie maatschappij kan opvragen.
Groet, Willem