Deze site geeft veel informatie over licht: Lichtstroom, lichtsterkte en verlichtingssterkte zijn begrippen die nogal eens worden gehanteerd en summier toegelicht. Ook berekeningen van de ene in de andere worden uitgevoerd. Dit artikel is een naslagwerk, waarnaar ik kan refereren vanuit andere artikelen.

Grootheden en eenheden
Ik start met een tabel, die de relevante begrippen aangeeft en deze summier uitlegt. Daarnaast kun je vanuit deze tabel naar de verschillende hoofdstukken voor meer uitleg.
| Grootheid (Nl) | Grootheid (Eng) | Eenheid | Toelichting, link |
|---|---|---|---|
| Uitgestraalde Stroom P | Radiant Flux | Watt | Voor lampen is dit het totaal van de straling, dus inclusief straling die wij niet kunnen zien, bijvoorbeeld infraroodstraling. Ik noem licht die straling wie we als mensen kunnen zien. |
| (Stralings)Helderheid | Intensity | W/sr | Helderheid van de uitgestraalde energie in een bepaalde richting. Is te berekenen uit de uitgestraalde stroom en stralingshoek. |
| Lichtstroom F of Φv | luminous flux | lm | Is een maat voor de hoeveelheid zichtbare energie die een lichtbron in alle richtingen uitzendt. Zie ook de voorbeelden. |
| Lichtsterkte Iv | luminous intensity | Cd = lm/sr | De hoeveelheid licht die een bron afgeeft in een bepaalde richting. Zie ook de voorbeelden. |
| Ruimtehoek | Solid Angle | steradiaal sr | Kegelvorm startend vanuit center van een bol. |
| Stralingshoek | Beam Angle | graden | Hoek waarmee licht uit een puntbron treedt. Zie ook de omrekening stralingshoek naar ruimtehoek. |
| Verlichtingssterkte Ev | Illuminance | lx | 1 lux is de lichtsterkte voorgebracht door 1 Cd op een opp. loodrecht op de lichtstralen op een afstand van 1 meter van de bron. Zie ook de voorbeelden.
Zie tevens ook de richtlijnen voor een minimale verlichtingssterkte in diverse situaties. |
Het is mogelijk om van een gemeten luxwaarde of van een gegeven intensiteitwaarde van een lamp, te komen tot een berekening van de lichtstroom. Ook te weg terug van lichtstroom naar verlichtingssterkte te gaan, mits je de stralingshoek kent of het stralingsdiagram. Zie hiervoor het omrekenhoofdstuk.
Ruimtehoek
We definiëren een ruimtehoek. Deze ruimtehoek wordt uitgedrukt in steradialen (sr), en 4 x pi sr is precies een gehele bol.
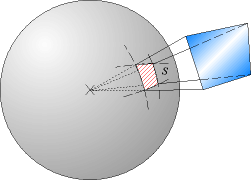
Figuur 1: een voorstelling van een ruimtehoek
Denk bijvoorbeeld een gloeilamp in het centrum van de bol. Een gloeilamp genereert naar iedere richting een redelijke constant uitgestraald vermogen. Dus wanneer het totaal aan uitgestraald vermogen bekend is van deze gloeilamp, dan delen we deze waarde door 4 x pi en dan hebben we de stralings helderheid die wordt uitgedrukt in Watt/steradiaal, oftewel W/sr. Let wel, sr is een dimensieloze eenheid. Ik schrijf hem erbij, om duidelijk te maken dat het hier gaat om een helderheid en niet om het vermogen of de stroom.
Bij een led is er echter geen even grote stroom naar iedere richting, maar is de stroom veel meer gefocusseerd in één richting. We moeten dan eerst de stralingshoek van de led weten.
Stralingshoek
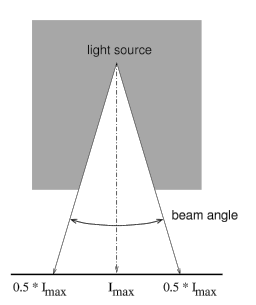
Figuur 2: een voorbeeld van een stralingshoek (Engels: beam angle)
Een stralingshoek is dan die hoek tussen twee tegenoverliggende richtingen van de stralingsas, waarvoor de intensiteit tot de helft gezakt is t.o.v. de maximum intensiteit.
Omrekening stralingshoek naar ruimtehoek
Stel dat de stralingshoek gegeven is, dan is deze om te rekenen naar sr. Hiervoor moeten we eerst wat meer rekenen.
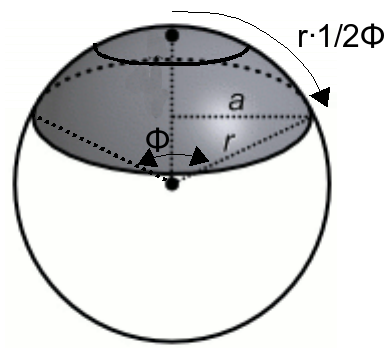
Figuur 3: hulpplaatje voor berekening ruimtehoek uit stralingshoek
Je ziet de stralingshoek φ, die de hoek van de kegel aangeeft. Deze kegel snijdt een denkbeeldige bol en het oppervlak wat van de bol dat binnen de kegel ligt, daarvan willen we de ruimtehoek weten. Allereerst berekenen we de oppervlakte zelf, door het sommeren van alle omtrekjes over de lijn r.1/2φ.
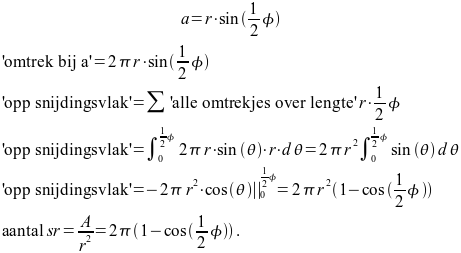
Formules 1: Van stralingshoek naar ruimtehoek in steradialen
Omrekening uitgestraalde stroom naar stralingshelderheid
Als bekend is wat het uitgestraalde vermogen van bijvoorbeeld een led is (in Watt in dit geval), en ook de stralingshoek is bekend, dan bereken de stralingshoek om in sr en deel het vermogen door het aantal sr en je hebt de stralingshelderheid. Bij leds worden nogal eens lenzen gebruikt. Deze zorgen dat het uitgestraalde vermogen in een kleinere stralingshoek worden “geperst” waardoor de stralingshelderheid toeneemt.
Lichtstroom F of Φv
De grootheid is gerelateerd aan de uitgestraalde stroom, echter alleen het licht (= zichtbare straling) wordt nu meegenomen.
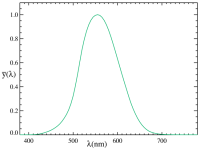
De observeerder zal een mens zijn, en de ogen van de mens zijn alleen gevoelig voor straling wanneer de golflengte ervan in een bepaald bereik ligt (400 – 700 nm). Dus van al het uitgestraald vermogen is alleen dat gedeelte van belang waarvoor het menselijk ook gevoelig is. Daarnaast is het menselijk oog niet even gevoelig voor alle licht in het bereik van 400 – 700 nm. Er is een set van curves opgesteld die de gevoeligheid van het oog voor bepaalde lichtgolflengtes weergeeft, in een goed belichte situatie waarbij we kleuren kunnen zien (photopic luminosity curve genaamd) en voor een weinig belichte situatie waarbij we geen kleuren kunnen zien (scotopic luminosity curve genaamd). Ik ga uit van de photopic luminosity curve omdat ik kleuren wil meenemen.
Figuur 4: Photopic liminosity curve; lichtgevoeligheid van het menselijk oog bij goede belichting
Dus van al het uitgestraalde vermogen is alleen dat gedeelte interessant wat wij kunnen zien. Dit leidt ons tot de definitie van lichtstroom (Engels: luminous flux) wat iets is als uitgestraald vermogen, alleen gecorrigeerd voor de gevoeligheid van het menselijk oog.
Voorbeelden lichtsterkte en lichtstroom
Stel je hebt een 100 W gloeilamp, die 1700 lumen aan lichtstroom genereert. Deze gloeilamp zal dit naar alle richtingen gelijk uitstralen (even geen reflector genomen achter de lamp) en dus is de helderheid 1700 lm / (4 x pi sr) = 135 Cd.
In een artikel over een 1000 lm led zie je dat een led met 1000 lumen en een hoek van 38° wel 2900 Cd oplevert. Dit echter alleen voor het gebied van die 38°. De led zal, wanneer ik me in de bundel van het licht bevindt en ernaar kijk, veel helderder zijn dan de 100 W lamp, terwijl deze laatste 1,7 x meer licht(energie) uitstraalt (verbruikt trouwens veel meer aan energie).
Nog een leuke, hoe helder is een InfraRood (IR) led?
Het antwoord is 0 Cd. Dit komt omdat het menselijk ook niet gevoelig is voor IR straling. Dus is er ook 0 lm lichtstroom.
Een kleine kanttekening is hierbij wel op zijn plaats. Een led zal niet alleen maar straling van één golflengte uitsturen (leds zijn niet monochromatisch), maar genereert straling met golflengtes over een klein gebiedje van het spectrum.
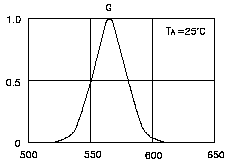
Figuur 5: Kleur vs intensiteit afkomstig van een typische groene led
De breedte van het gebiedje waar de led nog 50 % van de maximale intensiteit uitstraalt, wordt het “spectral line half-width” genoemd en geeft aan hoe monochromatisch de led is.
Bij IR leds geldt dit dus ook en er is wellicht een beetje straling dat nog in het zichtbare valt (= licht). Toch is het niet verstandig om over lm en Cd te spreken bij IR leds. De energiestraling van deze leds wordt dan ook in Watt uitgedrukt.
Verlichtingssterkte
Wanneer een lichtstroom een (denkbeeldig) oppervlak raakt, dan zegt men dat dit oppervlak verlicht wordt. De intensiteit van de verlichting, is de lichtstroom per oppervlakte-eenheid. Deze wordt de verlichtingssterkte Ev genoemd .
Er is nog een relatie tussen de verlichtingssterkte en lichtsterkte, namelijk:
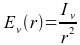
Formule 2: De verlichtingssterkte afhankelijk van de lichtsterkte en de afstand
Deze formule komt nog uit een application note van OSRAM over de OSTAR led, pagina 8. Hier zie je dus de afhankelijkheid van de afstand tot de lichtbron; bij een tweemaal zo grote afstand, wordt de verlichtingssterkte viermaal zo klein.
Voorbeeld verlichtingssterkte
Een bepaalde 100W gloeilamp straalt een lichtstroom uit van 1200 lm, evenredig verdeelt over een half boloppervlak. Bereken de verlichtingssterkte en de lichtsterkte op een afstand van 1 m en 5 m.
Antwoord:
Het oppervlak van een halve bol van 1 m straal is 2 x π x (1 m)2 = 6,28 m2.
De verlichtingssterkte op 1 m afstand is dan: Ev = 1200 lm / 6,28 m2 = 191 lm/m2 = 191 lx.
En op 5 m afstand: Ev = 1200 lm / (2 x π x (5 m)2) = 1200 lm / 157 m2 = 7,64 lx.
De ruimtehoek van een halve bol is 2 x π sr. De lichtsterkte is dan: Ir = 1200 lm / (2 x π sr) = 191 lm/sr = 191 Cd. Deze lichtsterkte hangt niet af van afstand.
Omrekeningen lichtstroom, lichtsterkte en verlichtingssterkte
Stel ik heb een led met een bepaalde lichtstroom (in lm). Nu is ook bekend wat de stralingshoek is. Dan is te berekenen wat de lichtsterkte is voor deze led. Bereken daartoe de stralingshoek om in sr, en deel het aantal lm door sr en je hebt de lichtsterkte.
Je kunt ook berekenen wat de verlichtingssterkte is op een bepaalde afstand. Neem daarvoor de lichtsterkte in die richting en deel deze door het kwadraad van de afstand.
Nu gelden deze berekeningen wanneer we uitgaan van een constante helderheid over een gebied als de stralingshoek. Dit is echter niet altijd zo, zie ook maar eens het stralingsdiagram van de OSTAR led met lens.
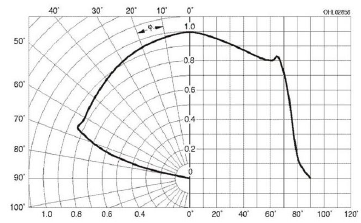
Figuur 6: Stralingsdiagram van OSTAR led met lens
Hier loopt de lichtsterkte langzaam af, totdat een hoek van 60 graden wordt bereikt en dan loopt de helderheid snel af. Als we nu de lichtsterkte weten op 0°, dan kunnen we bijvoorbeeld de lichtstroom berekenen. Als we nu de verlichtingssterkte weten op 0° en de afstand, dan kunnen we deze omrekenen naar de lichtsterkte (zie formule 2). En aangezien we nogal wat artikelen hebben waar we de verlichtingssterkte hebben gemeten van vele lampen, willen we nu deze kunnen omrekenen naar de lichtstroom.
De berekening gaat als volgt. Je weet het verloop van de lichtsterkte als functie van de hoek, en zet deze in een tabel, waarbij je van 0° tot 90° loopt, en bij iedere hoek zet je neer wat de lichtsterkte is.
Voorbeeld:
| hoek [graden] | lichtsterkte [Cd] |
|---|---|
| 0 | 104 |
| 5 | 98 |
| 10 | 97 |
| 15 | 96 |
| … | … |
| 80 | 20 |
| 85 | 10 |
| 90 | 0 |
Let op, het is nog beter om een regel per 1 graad te maken in een spreadsheet programma, dat geeft een nauwkeuriger resultaat. We gaan namelijk zodadelijk de waarde van de lichtsterkte constant houden voor het bereik van de ene regel naar de andere. Ik noem zo’n bereik een gebiedje. Zo is het eerste gebiedje het bereik van 0° tot 5°, en dit komt overeen met de top van een bol.
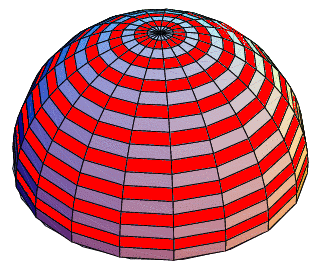
Figuur 7: Gebiedjes op een halve bol, aangegeven door 0° – 5°, 5° – 10° etc
Het gebiedje van 0° tot 5° ligt dus tussen het eerste rode circelschijfje in. Ik wil nu de oppervlakte van dit gebiedje berekenen en dat uitdrukken in sr. Ik houd voor dit gebiedje de lichtsterkte constant en bereken de vermenigvuldiging van lichtsterkte maal het aanstal sr voor het gebiedje van 0° tot 5°. Dit levert de lichtstroom op voor dit gebied.
Voor het gebiedje van 5° tot 10° bereken ik het aantal sr voor 0° tot 10° en haal er het aantal sr voor 0° tot 5° vanaf. Ik doe weer een vermenigvuldiging van de lichtsterkte voor dit gebied van 5° tot 10° met het aantal sr en ik heb de lichtstroom voor dit gebied.
Ik doe dit voor alle gebiedjes totdat ik aangekomen ben bij gebieden waar de lichtsterkte toch al nul geworden was. Daarna sommeer ik de lichtstromen voor alle gebiedjes en heb ik de totale lichtstroom. Een voorbeeld van een tabel met alle berekeningen voor een paar bestaande type OSTAR leds van OSRAM gaat hierbij. Ik had van deze leds de lichtsterkte zowel als het stralingsdiagram. Dit heb ik gebruikt om de lichtstroom uit te rekenen en daar ook de lichtstroom was gegeven van deze leds, kon ik de berekening controleren. Blijkt dat ik met een benadering van 1 graad (dus gebiedjes van 1° tot 2° etc) beter uitkom en dicht in de buurt van de door de fabrikant gegeven waardes.
Efficiency
Nu is het mogelijk om alle meetgegevens van de verlichtingssterktes (in lux) van verschillende lampen op deze site, om te rekenen naar lichtstroom (zoek op lampmetingen op deze site). Als nu ook het vermogen bekend is van de lamp, dan de efficiency bepaald worden. Dit wordt dan uitgedrukt als de deling van lichtstroom in lumen door het verbuik in Watt. Hier kan ik in een ander artikel eens op terugkomen.
Richtlijnen voor verlichtingssterkte
Op het internet zijn voorbeelden te vinden van hoeveel verlichtingssterkte er nodig is om een bepaald type activiteit uit te kunnen voeren. Een mooie lijst is te vinden op de site van De Belsgische Federale Overheidsdienst, waar de minimale verlichtingssterkte wordt gegeven voor bepaalde activiteiten.
Om te voorkomen dat deze link eens verloren raakt, hierbij nogmaals de lijst:
Onderstaande tabel bepaalt de minimum verlichtingssterkte, in lux uitgedrukt, voor de verschillende plaatsen, werkzaamheden en toestellen, behoudens voor de in artikel 59, eerste lid van het A.R.A.B., bedoelde verrichtingen.
Die verlichtingssterkte geldt voor het werkvlak of, indien dit niet juist kan worden bepaald, voor een horizontaal vlak dat 0,85 m boven de grond ligt.
Wat de in littera’s a), b) en c) van onderstaande tabel genoemde plaatsen betreft, geldt die verlichtingssterkte, gemeten ter hoogte van de grond, evenwel voor het vlak dat loodrecht op de lichtstroom staat.
a. 2 lux:
Rangeerstations van de spoorwegen, op de plaatsen waar het personeel dient te komen, met uitzondering van de eigenlijke rangeeremplacementen.
b. 10 lux:
Eigenlijke rangeeremplacementen van de spoorwegstations, dit zijn emplacementen die zich uitstrekken van de rangeerheuvel, met inbegrip van deze, tot en met de laatste verspreidingswissels.
Binnenplaatsen en buitengelegen doorgangen.
c. 20 lux:
De volgende, buiten de gebouwen gelegen plaatsen: stations voor transformatie van elektrische stroom, laad- en losplaatsen waar niet wordt gewerkt, alsmede alle andere plaatsen van analoge aard.
d. 50 lux:
De volgende, binnen de gebouwen gelegen plaatsen: doorgangen, exclusief die in de warenhuizen, gangen, trappen, pakhuizen, opslagplaatsen en magazijnen voor ruwe of omvangrijke materialen, garages, alsmede alle andere plaatsen van analoge aard.
Koelkamers.
Werkzaamheden die geen enkele waarneming van de details vergen: behandeling van grove materialen (kolen, as, enz.), ruwe sortering, breken van leemhoudende producten, grof werk of ruwbouw op scheepswerven en bij werken van burgerlijke bouwkunde, alsmede alle andere werkzaamheden van analoge aard.
e. 100 lux:
Werkzaamheden die slechts een geringe waarneming van de details vergen: fabricage van half afgewerkte ijzeren of stalen producten, ruwe assemblage, malen van graan, uitpakken, sorteren en kaarden van wol, alsmede alle andere werkzaamheden van analoge aard. Machinekamers, stookplaatsen, personen- en goederenliften, pakkamers, lokalen voor ontvangst of verzending van goederen, laad- of losplaatsen waar gewerkt wordt, opslagplaatsen en magazijnen voor middelmatige en fijne materialen, alsmede alle andere plaatsen van analoge aard.
Kleedlokalen, toiletten, wasgelegenheden, eetvertrekken en andere plaatsen van analoge aard.
f. 200 lux:
Werkzaamheden die een matige waarneming van de details vergen: gewone assemblage, machinaal fatsoeneren, bewerken van niet-geverfde textiel en niet-geverfd leder, inblikken van levensmiddelen, versnijden van vlees, bewerken van hout op werkbanken, walsen en knippen van werkstukken met grote afmetingen, monteren en uitdeuken van koetswerk, alsmede alle andere werkzaamheden van analoge aard.
Doorgangen in warenhuizen.
g. 300 lux:
Werkzaamheden die een tamelijk scherpe waarneming van de details vergen: gewoon werk aan machines, precisieproeven, classificatie van meel, afwerken van leder, bewerken van niet-geverfde katoen, wol, zijde en kunstvezels, allerhande kantoorwerk, met inbegrip van intermitterend typewerk, confectiewerk behalve naaien en controle op de afwerking, herstellingen in garages, alsmede alle andere werkzaamheden van analoge aard.
Schakelborden, weegtoestellen, toetsenborden en andere toestellen of inrichtingen van analoge aard.
h. 500 lux:
Werkzaamheden die een scherpe waarneming van de details gedurende een lange tijd vergen: nauwkeurige assemblage, nauwkeurig werk aan machines, polijsten en afschuimen van glas, precisiewerk in de glasfabrieken, teken- en mecanografiewerk, permanent typewerk, bewerken van geverfde textiel en geverfd leder, fijn laswerk alsmede alle andere werkzaamheden van analoge aard.
Toonbanken.
i. 700 lux:
Werkzaamheden die een zeer scherpe waarneming van de details vergen: bewerken van geverfde katoen, wol, zijde en kunstvezels, teken- en mecanografiewerk, waarbij een bijzonder grote verlichtingssterkte nodig is, alsmede alle andere werkzaamheden van analoge aard.
j. 1 000 lux:
Werkzaamheden die een uiterst nauwkeurige waarneming van de details vergen: zeer nauwkeurige assemblage, beproeven van zeer gevoelige instrumenten, juweliers- en horlogemakerswerk, classificeren en sorteren van tabak, zetwerk, en nalezing van drukproeven in drukkerijen, naaien en controle op de afwerking in de confectieateliers, monteren van uiterst fijne onderdelen, bereiden, doseren en vermengen van kleurstoffen, alsmede alle andere werkzaamheden van analoge aard.
Wanneer het niet mogelijk is met preciesheid de werkplek of het werkvlak te omschrijven mag de nodige verlichting, op advies van het Comité voor Preventie en Bescherming op het Werk of, bij ontstentenis van zulk Comité, van de Dienst voor Preventie en Bescherming op het Werk, worden bepaald en gemeten overeenkomstig de norm NBN 255 – leidraad voor de verlichting in de industrie. Het advies van dat comité of, bij ontstentenis van zulk comité, van die dienst, moet eveneens worden ingewonnen om te beslissen over de lichtsterkten die moeten worden voorzien in de gevallen die niet zijn gegeven in artikel 62 van het A.R.A.B..
Elke installatie en elk toestel voor algemene of lokale verlichting moet zo gebouwd en geplaatst zijn dat gevaarlijke of hinderlijke verblindende lichtuitstralingen, stroboscopieverschijnselen, oververwarming van de lokalen en luchtbederf worden vermeden.
Nog een extra uitbreiding op de lijst is deze tabel, die een uittreksel geeft van de NEN2443 norm die gaat over functionele en prestatie-eisen voor parkeerterreinen en parkeer- en stallinggarages voor personenauto’s.




27 reacties op “Licht grootheden uitgelegd”
Super duidelijk en degelijk artikel. Begrijp nu wat al die waarden betekenen. Kan zo op wikipedia… (misschien nog iets toevoegen over het verschil tussen warm en koud wit licht)
Marcel, I’m really impressed with the depth of your study and the excellent graphics of your article. This article looks like one of your best ones yet. Have you considered publishing it? (In English, perhaps?)
Goed artikel, dit maakt een hele hoop duidelijk. Het is elke keer weer genieten wanneer er een nieuwe staat op deze site.
Nog wel een kleine opmerking m.b.t. ‘onzichtbaar licht’ en ‘infrarood licht’: die bestaan niet, omdat licht per definitie een voor mensen zichtbare straling is. Formeel moet je dus praten over infraroodstraling en onzichtbare straling.
Tweemaal bedankt Wally. Voor de opmerking en het compliment. Ik heb het artikel nog eens doorgenomen en zo goed mogelijk de woorden straling en licht toegepast.
een bolvormige gloeilam heeft een specifieke lichtstroom van 18lm/w en een lichtsterkte van 86 cd was is de verlichtings sterkte op een afstand van 0.6 meter
andwoord graag naar mijn email sturen
Juan_morais@hotmail.com
@ Juan
Je geeft aan de lichtsterkte is 86 Cd. Ik ga er nu vanuit dat deze lichtsterkte constant is over alle richtingen. Dan komt 86 Cd aan lichtsterkte overeen met 86 lx op 1 m. Je wilt het weten op 60 cm afstand, dat wordt dan 86 lx/(0.6 x 0.6) = 240 lx.
Dan nog meer. Je praat over 86 Cd aan lichtsterkte, wat 86 lumen/sr is. Aangezien er over een bol 2 x PI sr zijn, is dus de totale lichtstroom 540 lm (aangenomen dat de lichtsterkte constant is over de gehele bol). Met een gegeven efficiëncy van 18lm/W kom ik uit op een 30 W lamp. Klop dit?
weet niet staat niet gegeven maar dank je voor je antwoord
ok ik heb nog een vraag
een gloeilamp heeft een verlichtingsterkte van 400 lx op een afstand van 3 meter. hoe groot is de verlichtingssterkte op 4 meter ?
@ Juan:
400 lx op 3 meter, dan volgt
( 3 x 3 ) / ( 4 x 4 ) x 400 lx = 225 lx op 4 meter.
Zie tevens het volgende artikel over de OliNo lampmeetopstelling, daar staat de formule nog eens uitgewerkt met een voorbeeld (onder het hoofdstuk “Lux op 1 meter afstand”).
Het is het makkelijkst om te onthouden dat verder weg, er ook minder lux overgehouden wordt. En als je onthoudt dat het verband kwadratisch is, dan weet je wat je in de teller (boven de deelstreep) en wat in de noemer (onder deelstreep) moet zetten. Het verband is juist kwadratisch, omdat de hoeveelheid licht verdeeld wordt over een oppervlakte, en bij een bij een afstandstoename van 2x wordt de oppervlakte 4x zo groot. Aangezien de hoeveelheid licht niet verandert, wordt dus de hoeveelheid licht per oppervlakte 1/4e.
op een ruimte van 8m op 4m waar en hoeveel spots moet men plaatsen om een ideale verlichting te verkrijgen
@ Kris
Ik heb in dit artikel iets daarover uitgelegd. Het komt erop neer dat je uitgaat van de mate van verlichting van 1 lamp op een plat vlak onder de lamp. Wanneer je nu in de nabijheid van deze lamp eenzelfde lamp hangt die op hetzelfde vlak schijnt, dan tellen de verlichtingssterktes (E_v in lux) bij elkaar op. Als je nu wilt dat je 400 lx hebt, dit om goed te kunnen lezen bijvoorbeeld, dan moet je het profiel kennen van E_v van een bepaalde lamp op een vlak, en dan kun je berekenen hoever de lampen uit elkaar moeten staan zodanig dat de som van de E_v van ieder lamp, op ieder plek op het platte vlak rond die 400 lx komt.
Volg de link eens die ik je geef. Als je een voorbeeld wilt, laat me dan eens weten welke lamp je wilt hebben, en welke E_v in lux je op het vlak wilt hebben. Dan kan ik wel eens inschatten hoever de lampen t.o.v. elkaar moeten staan en hoever de lampen van het te verlichten vlak mogen staan.
Let wel, die door mij genoemde 400 lx is een mooie waarde waarbij je kunt lezen. Als je dat niet hoeft, dan kun je ook met lagere waardes toe, bijvoorbeeld 100 lx.
Het hangt er dus vanaf waar je je ruimte voor wilt gebruiken.
Beste Marcel,
Je zegt dat de verlichtsterkte gelijk is aan de lichtsterkte gedeeld door de afstand in het kwadraat. Maar lichtsterkte wordt uitgedrukt in cd en lux is gelijk aan lm/m²… maar cd en lm, is toch een verschil, dus volgens je formule zou je eigenlijk cd/m² moeten hebben… en toch niet lm/m²?
Alvast bedankt!
Mvg, Maarten
Beste Maarten,
Allereerst een hele goede vraag. Ik hoop dat ik je met onderstaande kan helpen. Je verwijst naar de formule:
E_v (r) = I_v / r^2.
Helderheid I_v is niet afhankelijk van de straal r. Dit komt omdat helderheid I_v gedefinieerd is als lumen per sterradiaal. Dus ga ik verder weg, dan heb ik met een constante sterradiaal ook een groter oppervlak waarover ik moet integreren. Ik weet dat de verlichtingssterkte afneemt in het kwadraad met de afstand, dus voor de helderheid I_v blijft de waarde hetzelfde. Vandaar dat je ook I_v in de formule ziet staan zonder een afhankelijkheid van r.
Nu even E_v (r). Deze is dus wel afhankelijk van de straal r en neemt dus af met het kwadraad. Maar op r = 1 meter, dan zijn E_v (1) en I_v kwa getalswaarde aan elkaar gelijk. Dit komt omdat op r = 1 meter, een sterradiaal precies 1 m^2 is aan oppervlakte, en op E_v (1) = lumen / m^2. Daar wordt dus E_v gelijk aan I_v!
Je hebt gelijk dat kwa eenheid de formule niet klopt. Maar getalsmatig klopt deze wel. Vul maar r = 1 m in, dan volgt: E_v (1) = I_v en dat klopt, omdat lumen/sr op r = 1 m gelijk is aan lumen/m^2.
Wat ik doe met deze formule is gewoon de helderheid uitrekenen. Dus ik heb een E_v waarde op bijvoorbeeld 105 cm afstand (een standaard afstand voor mijn meetbuis), dan reken ik de E_v om naar 100 cm afstand (dit is een factor 100^2 / 105^2 kleiner) en dat noem ik dan ook meteen I_v.
Beste Marcel,
Vriendelijk bedankt voor de uitleg! Ik was je btw in de vorige post vergeten te bedanken voor het goed artikel. Maar kan jij me soms goed het verschil tonen tussen de openingshoek en de ruimtehoek.
Alvast bedankt!
Mvg, Maarten
Hee, ik zit dit allemaal door te lezen, en ik gok dat je dit met een voorgaande studie allemaal te weten bent gekomen?
of is deze kennis allemaal door eigen onderzoek gekomen?
iig, ik vind het een machtig goed artikel en vroeg me af heb je een studie hiervoor gevolgd, zo ja welke ?
en zou je me dat dan kunnen mailen, want ik ben bang dat ik deze site niet zo makkelijk kan hervinden thuis (nu op’t werk)v_martin_v@hotmail.com
mvg. martin
ik heb mezelf de site ge-maild 😉 ik kan het nog teruglezen als je ff geen zin hebt in mailen 😀
ohw je hebt al gemaild .. Dankje 😉
Hallo lezers,
Ik zit me hier te verdiepen en ik zie door de bomen het bos niet meer.
Ik heb op internet mooie verlichting gezien die ik straks wil gebruiken in mijn nieuwe keuken aan het aanrecht zodat we goed licht hebben bij het koken.
Wat ik weet is dat de lichtopbrengst 54 lm is met een lichthoek van 120 graden. (zie de weblink).
Mijn vraag is nu of dit te veel, te weinig of genoeg licht is.
Alvast bedankt voor de reacties.
Ook ik zie door de bomen het bos niet meer, dus maar even de korte versie van de vraag: Aan mijn schuur hangen ter verlichting van de tuin de volgende lampen:
1 X KONSTSMIDE BOLZANO 7595 7595-000 via een timer, en twee maal KONSTSMIDE BOLZANO 7594 wandlamp via een klikaanklikuit Inbouw dimmer/schakelaartype ACM-300.
In de lamp via de timer zitten 2 x 35W halogeen GU10, in de lampen via de dimmer elk 1 x 35W halogeen GU10.
Nu vindt ik 140Watt nogal wat, dus wil ik hier energiezuiniger mee omgaan, dus LED was de gedachte.
Maar welke lamp is dan de meest voor de hand liggende.?
Hans, Luc,
Ik denk niet dat het voor Olino debedoeling is om bepaalde lampen te adviseren. Sterker nog ik denk dat ze dan hun geloofwaardigheid als onafhankelijk zullen verliezen.
Ik weet niet hoe handig jullie zijn met de PC maar als je het programma DiaLux download (gratis) dan kun je de ruimte die je wilt verlichten globaal intekenen. Met de Eulumdat files die bij elke lamp op deze site gepubliceerd worden kun je dan kijken wat een bepaalde lamp doet voor jouw opstelling. De software is niet zo heel moeilijk in het gebruiken.
Luc, advies voor in de keuken. Kijk voor lampen met een hoge CRI/RA waarde (>80) zodat je de kleur van het eten goed kunt zien. Zou niet leuk zijn als je denkt dat je gasten een mooi rood stukje vlees serveert terwijl die zwart geblakerd blijkt. (reff.: mijn eigen kookunsten). Denk ook dat je moet richten op 400lux op je keukenblad/werruimte.
prachtig artikel, maar ik ben geen deskundige op dit gebied.
Wel bij dat ik een groep deskundige mensen heb gevonden.
Ik ben aan een project bezig waarin ik zeer felle led’s gebruik als signalisering op een zweefvliegveld, maar ik zit vast. De doelstelling die ik voor ogen had kan ik maar deels waarmaken, maar van opgeven wil ik niet weten.
Is er hier iemand die het ziet zitten om eens te luisteren naar mijn verhaal en me mogelijk terug met de neus in de juiste richting te zetten?
Met vriendelijke groeten
Martin
Beste Marcel,
Goed artikel! Maar ik heb helaas nog geen antwoord op mijn probleem gevonden. Kan je mij helpen om te rekenen van radiant flux (watt/m2) naar illuminace (lux). Het gaat om licht van rode leds met een golflengte van 627 nm.
Met vriendelijke groet,
Bas
Ik heb m’n antwoord gevonden op:
http://hyperphysics.phy-astr.gsu.edu/hbase/vision/lumpow.html
Hoi Bas,
De link die je geeft gaat uit van een gewone gloeilamp. Die geeft een heel spectrum af en in de link gaat men uit van 17lm/W. Echter voor jou gaat dat niet op, jij hebt het over rood licht van 627 nm.
De omrekening gaat dan als volgt:
X [W/m^2] * 683 [lm/W@555nm] * 0.2998 (licht effectiviteit bij deze frequentie).
(zie ook de efficacy table http://hyperphysics.phy-astr.gsu.edu/hbase/vision/efficacy.html#c1 )
Hoi Marcel als 1ste wil ik even laten weten dat ik een leek ben op gebied van licht electra.
Maar der is me gevraagd een werkplaats van 1150m en 6 meter hoog van een systeem plafon en van 700 lux lichtsterkte te voorzien.
Hoe bereken je dan hoeveel armatuur je nodig hebt en wat voor licht kun je het beste kiezen?
Grt
gebruik de volgende grove formule:
aantal armaturen x netto lichtstroom uit 1 armatuur / oppervlakte kamer.
let op, wel de netto lichtstroom per armatuur.
Beste Marcel, ZEER – ZEER interessant artikel met uitleg voor professionelen en andere.
Zelf ben ik al 10 tallen jaren actief in (hoofdzakelijk industriële) verlichting. U geeft “Richtlijnen voor verlichtingssterkte” gaande van a=2 Lux tot j=1.000 Lux. Uit ervaring weet ik dat HEEL veel mensen een welbepaalde Lux-waarde niet of moeilijk kunnen relativeren, m.a.w. wat moet ik me voorstellen met 100 of 1000 Lux. Ik geef dan volgende -voor zich sprekende- voorbeelden.
Bij een zeer heldere maneschijn hebben we +/- 2 Lux (hierbij zijn de kegeltjes in onze ogen niet actief waardoor we geen kleuren kunnen onderscheiden en enkel wit-grijs-zwart zien), bij daglicht met volle zomerse zon is dit al gauw 50.000 tot 80.000 Lux en meer in zuiderse regionen.
Dat deze grote verschillen in “onze waarneming” van verlichtingssterkten niet evenredig zijn de reële gemeten waarden komt door het feit dat de pupil van onze ogen varieert van +/- 2 tot 7 mm weliswaar met een relatief traagheid.
Er zijn nog zoveel andere “menselijke aspecten” in verband met licht !!!!
Het zou interessant zijn als een man zoals u, met dergelijke kennis en wetenschap hieraan een artikel zou schrijven. NB : Ik wil het met u wel eens hebben over dergelijke aangelegenheden … uit ervering.
MVG
Valère Bers
VALumax bv